Példák a sorozat megoldások, magasabb matematika

Példa. A tanulmány a konvergencia és az összeg a sorozat.

Adott: egy szám
Keresés: összege sorozat esetében a konvergencia.

Mi jelent a tagok számának összege két szempontból:

Kiderült, hogy az n-edik részösszegként a sorozat felírható:

Ebből következik, hogy.

A sorozat konvergál. Számos összegével egyenlő.

Példa. Egy szükséges kritériuma konvergenciájának sorozat.

Adott: egy szám
Keresés:
Ellenőrizze, hogy a szükséges jele konvergencia sorozat.

Szükséges attribútum konvergencia a sorozat abban a tényben rejlik, hogy ha a numerikus sorozat konvergál,
Ennek következtében, ha a ≠ 0, akkor a sorozat eltér.

Egy adott feladat egy számsorozat:
≠ 0. Számos eltérő.

Példák. Elegendő, ha a konvergencia pozitív sorozat.

Adott: soraiban
1)
2)
3)
4)
5)

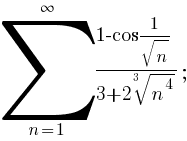
6)
Keresés:
Fedezze fel a konvergencia a sorozat.

1) Azon a tényen alapul, hogy az összes ≤ n és generalizált harmonikus sor konvergál, ebből következik, hogy kisebb számú konvergens tagok.

2) Azon a tényen alapul, hogy ha a feltételek teljesülnek: ln n ≥ 0 n ≥ 1, majd ≥ n ≥ 1.
Az általánosított harmonikus sor divergens, ezért számos nagy tagok eltérő.

3) a több különálló fő része az N-edik tag: amint n → ∞ ∼ .
Egy előre meghatározott számú és számos azonos viselkedést.
Mértani sor konvergens, akkor sorozat konvergál.

4) válasszon a számos a fő része a n-edik tag: amint n → ∞ ∼ .
megbízás <1, поэтому ряд расходится.

5) a több

Kiemeljük a fő része a n-edik ciklus a sorozat:
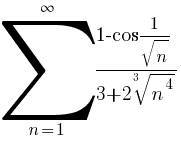
ha n → ∞ ∼ .
Az, hogy a> 1, tehát a sorozat konvergál.

6) A sorozatból kiemelje a fő része a n-edik ciklus a sorozat:
ha n → ∞ ∼
Az eljárás tehát a sorozat eltér.