Teljesítmény funkció - studopediya
Funkció ahol x - változó, egy - egy adott számú, az úgynevezett a teljesítmény függvényt.
Ha valami - egy lineáris függvény, annak grafikon - egy egyenes vonal (lásd 4.3, 4.7 ábra ..).
Ha valami - másodfokú függvényt, annak grafikon - egy parabola (lásd 4.3, 4.8 ábra ..).
Ha a gráf - a köbös parabola (lásd 4.3, 4.9 ábra ..).
Ez az inverz függvénye
1. Mező meghatározások:
2. Az értékrend:
3. A paritás páratlan: páratlan függvény.
4. gyakorisága funkciók: nem periodikus.
5. A nullák: X = 0 - egy nulla.
6. Maximális és minimális értékek a funkció: a legnagyobb és a legkisebb érték a függvény nem rendelkezik.
7. Az időközönként növekedését és csökkenését: a funkció növeli a saját domain.
8. A grafikon a köbös parabola szimmetrikus grafikus tiszteletben a y = x és képviseli ábrán. 5.1.
1. Mező meghatározások:
2. Az értékrend:
3. A paritás páratlan: a funkció még.
4. gyakorisága funkciók: nem periodikus.
5. A nullák: egyedülálló nulla x = 0.
6. Maximális és minimális értékek a függvény: veszi a legkisebb érték az x = 0, és értéke 0.
7. Az időközönként növekedését és csökkenését: a funkció csökken az intervallum, és egyre nagyobb a szakadék
8. ütemezés funkció (minden n Î N) «mint» a grafikonon egy másodfokú parabola (grafikonok funkciók ábrán mutatjuk be. 5.2).
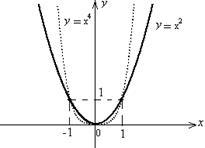
1. Mező meghatározások:
2. Az értékrend:
3. A paritás páratlan: páratlan függvény.
4. gyakorisága funkciók: nem periodikus.
5. A nullákat a funkció: X = 0 -uniqueness nulla.
6. Maximális és minimális értékek maximális és minimális értéke a függvény nem semmilyen
7. Az időközönként növekedését és csökkenését: a funkció növeli a saját domain.
8. ütemezés funkció (mindegyik), „hasonló” a grafikon a köbös parabola (grafikus funkciók ábrán látható. 5.3).
1. Mező meghatározások:
2. Az értékrend:
3. paritás, és Odd: A funkció nincs tulajdona paritás és furcsa.
4. gyakorisága funkciók: nem periodikus.
5. A nullákat a funkció: X = 0 -uniqueness nulla.
6. Maximális és minimális függvény értékei: A legkisebb értéke 0, a függvény a pont x = 0; leginkább releváns.
7. Az időközönként növekedését és csökkenését: a funkció növeli a saját domain.
8. Minden ilyen függvény egy bizonyos index inverze biztosított funkciók
9. Graph „mint a” funkciót a függvény grafikonját minden n és ábrán mutatjuk be. 5.6.
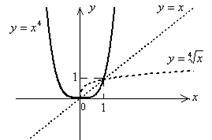
1. Mező meghatározások:
2. Az értékrend:
3. A paritás páratlan: páratlan függvény.
4. gyakorisága funkciók: nem periodikus.
5. A nullák: X = 0 - egy nulla.
6. Maximális és minimális értékek a funkció: a legnagyobb és a legkisebb érték a függvény nem semmilyen
7. Az időközönként növekedését és csökkenését: a funkció növeli a saját domain.
8. A függvény grafikonját ábrán látható. 5.7.
1. példa Plot a jellemzők:
Határozat. 1) felrajzolásához ez a funkció segítségével egy grafikon transzformációs szabályok:
a) az épület egy függvény grafikon (ábrán látható 5,7) .;
b) megkapjuk a grafikon a grafikon funkció párhuzamos átvitel, hogy egy egység a jobb az X tengely mentén, és két egység lefelé az Y tengely mentén;
c) a menetrend az eredeti funkció nyert grafikon a tartalék részét a jobb oldali grafikonon a y-tengely és az Y-tengely. Egyéb - a visszaengedett (5.8 ábra azt szaggatott vonallal mutatjuk be.). A fennmaradó része a grafikon szimmetrikus kiegészítik azt képest az y-tengelyen (ábra. 5.8).
2) Átalakítás a funkciót a formában Megjegyezzük, hogy a grafikon e funkció úgy kapjuk meg, a következő átalakítások:
a) össze egy grafikon a függvény
b) A grafikon nyerik az előző leképezési szimmetrikus tengelyéhez Oy;
c) megkapjuk a függvény grafikonját az előző ellensúlyozta 4 egység a végig az x-tengely;
g) egy előre meghatározott függvény grafikon nyerik a grafikon egy párhuzamos elmozdulását a két egység le az y tengely mentén (ábra. 5.9).