sűrűségfüggvénye

Folytonos. a. Megadhat egy funkciót, amely az úgynevezett sűrűség eloszlását vagy a valószínűség sűrűség vagy a differenciális eloszlásfüggvény.

sűrűségfüggvényt folyamatos. a. X nevezzük f (x) - az első származékot az eloszlási függvény F (x):

Ebből a meghatározásból következik, hogy az eloszlás a primitív sűrűség eloszlását.

Ahhoz, hogy leírják a diszkrét valószínűségi eloszlás. a. eloszlást nem alkalmazható.

A valószínűségi jelentését sűrűség eloszlását.

Így a határ az arány a valószínűsége, hogy egy folytonos p. a. értéket veszi fel tartozó intervallum (x, x + Ax), a hossza és ezen intervallum (ha Ax → 0) egyenlő az érték a sűrűség eloszlása ​​a ponton x.

A sűrűség függvény jellemzi minden érték folyamatos véletlen változó egyedileg, ahelyett, egy sor, mint a helyzet az eloszlásfüggvény.

Találati esélyét folyamatos. a. előre meghatározott időközönként.

Szerint a Newton - Leibniz:

Megtalálni a eloszlásfüggvénye egy ismert sűrűségű funkciót.

Elhelyezés az előző képlet a = -∞, b = x, és cseréje az integráció az X változó értékét t, van:

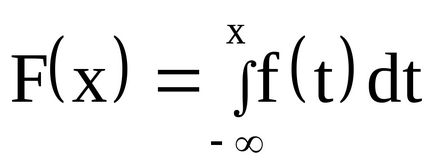
Tulajdonságok valószínűségi sűrűség

Tulajdonság 1. A sűrűsége eloszlás - negatív funkció: f (x) 0 (például eloszlásfüggvény - nem csökkenő függvény, és az elosztó sűrűsége az első deriváltját).

Bizonyítás. helytelen szerves

Ez fejezi ki az esemény valószínűsége, hogy a valószínűségi változó, akkor az értéke tartozó intervallumot (-∞, ∞). Nyilvánvaló, hogy egy ilyen esemény biztosan ezért a valószínűsége annak egységét.

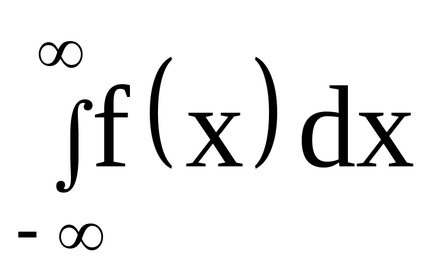
Geometriailag ez azt jelenti, hogy az egész terület a görbe vonalú trapéz által határolt tengely 0x és az eloszlási görbe egyenlő egy.

Vchastnosti ha minden lehetséges értékei valószínűségi változó tartozik az intervallumot (a, b) a

.

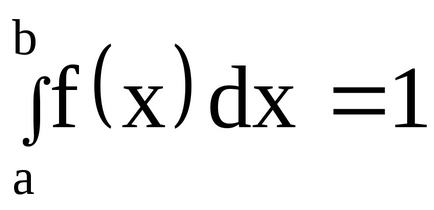
Lehetséges idővonal sűrűség eloszlása ​​(példa)

f1 (x) - sűrűsége nyert összeg az 1. játék

f2 (x) - sűrűsége A nyeremény összege a második játék

Milyen játékot előnyös?

Numerikus jellemzőit valószínűségi változók.

Ezek a jellemzők lehetővé teszik, hogy megoldani sok problémát anélkül, hogy ismernék a törvény eloszlás valószínűségi változók.

Jellemzői a véletlen változó helyzetben a valós tengelyen.

Az elvárás az, ez a súlyozott átlag értéke az X valószínűségi változó, ahol az abszcisszán az egyes pont xi tartalmazza a „tömeg” egyenlő a megfelelő valószínűségek.

A matematikai elvárás néha egyszerűen csak átlagos értékét rv

A diszkrét véletlen változó

Folyamatos véletlen változó

Divat - a legvalószínűbb értéke a valószínűségi változó (azaz amelyek esetében a valószínűségi sűrűség eloszlása ​​vagy pi f (x) eléri a maximális.).

Megkülönböztetni egymóduszú eloszlás (egy mód), multimodális eloszlás (több üzemmód) és animodalnye (nem divat)