menyasszony tétel, matematika, online megoldást!

Azt hiszem, nagyon kevés ember tudott néhány elmélet lesz szó, ítélve csak a cikk címe. Ma beszéljünk az egyik legfontosabb tétele a geometria - „Pitagorasz-tétel”. Köztudott, hogy szinte mindenki, és nem csak annak alkalmazására, hanem egy csomó más történet kapcsolódik hozzá, az a neve a bölcs Teremtő, valamint egy csomó bizonyíték. Az alábbiakban felsoroljuk az összes érdekes tény, hogy tanultam.

Bizonyára mindenki tudja, annak megfogalmazása, de csak abban az esetben, hozd újra:
„Egy derékszögű háromszög, a tér a átfogója egyenlő a négyzetének összege a másik két oldala.”

Hogy elmondani, hogy miért hívják „tétel a menyasszony.” A tény az, hogy az „Elements” Euclid még mindig nevezik „a tétel nimfák.” egyszerűen rajz nagyon hasonlít pcholku vagy pillangó, és a görögök nevezték nimfák. De amikor az arabok lefordított ez a tétel, a gondolat, hogy a nimfa - egy menyasszony. És ez így jött ki „menyasszony tétel”. Ezen kívül Indiában, ez az úgynevezett „szabály a kötelet.” Ez megy azzal a ténnyel, hogy ha valami épült, az építési közvetlen Kuta használtak egy kötelet, amely három részre osztottuk. Például, figyelembe 12 m és megkötve az egyik végén egy színes sáv 3 m, és a másik után 4 m, azaz a 3 és 4 m - ez lesz a lábak (közvetlen kuta oldalán), és 5 m - átfogója. A „híd szamár” nevezte ezt a tételt Németországban és Franciaországban.

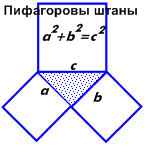
Van egy csomó komikus megfogalmazása ennek a tételnek:
* * *
Pitagorasz-nadrág
Minden oldalról egyenlő.
* * *
Ha egy háromszög adott nekünk
Sőt, a derékszög,
A tér átfogójának
Mindig könnyű megtalálni:
A lábak a téren felálló,
Találunk egy összeget hatáskörök
És ilyen egyszerű módon
Az eredmény jöttünk.
* * *

Ezért szeretném megjegyezni, hogy ez a tétel a legtöbb bizonyíték, Wikipedia szerint, ő számukra már 367. És alapuló készítmény bizonyult további tételei. És bár azt mondják, hogy egy ilyen tulajdonság derékszögű háromszög kitalálta, még jóval azelőtt, Püthagorasz.

Oszd meg barátaiddal:

Értékeld ezt a cikket: