Hogyan lehet megtalálni a maximum vagy minimum egy másodfokú függvény

Sok feladatot kell számítani a maximális, illetve minimális értékét a másodfokú függvény. A maximális vagy minimális lehet találni, ha a kezdeti funkció rögzítik a szabványos formában: f (x) = ax 2 + bx + c + bx + c>, vagy a koordinátáit a csúcsa a parabola: f (x) = a (x - h) 2 + k + k>. Sőt, a maximális vagy minimális bármely másodfokú függvény kiszámítható matematikai műveleteket.

lépések szerkesztése

1. módszer 3:
Másodfokú függvény van írva a szokásos formában szabályok

Record funkció szabványos formában. Másodfokú függvény - függvényében az egyenlete, amely tartalmaz egy variábilis x 2>. Az egyenlet esetében, vagy lehet, hogy nem tartalmaznak olyan x változó. Ha az egyenlet tartalmaz egy változót kitevő nagyobb, mint 2, akkor nem írja le a másodfokú függvény. Ha szükséges, hogy hasonló kifejezések, és mozgassa őket, hogy írjanak egy függvényt formanyomtatványon. [1]

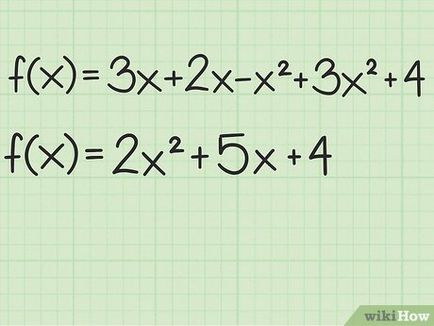
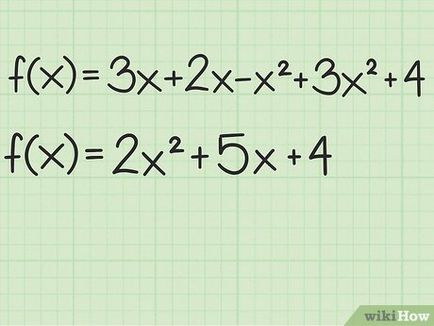
• Például, egy adott f (x) = x 3 + x 2 - x 2 x 3 + 2 + 4 + 3x ^ + 4>. Fold tagjainak változó x 2> és tagok az x változó. írni az egyenletet formanyomtatvány:
  • f (x) = 2 x 2 + x 5 + 4 + 5x + 4>

Határozza meg az irányt a parabola. A grafikon a másodfokú parabola. parabola ága felfelé vagy lefelé. Ha az együttható, x 2> pozitív parabola felfelé. Ha negatív együtthatót, a parabola lefelé irányul. Például: [2]

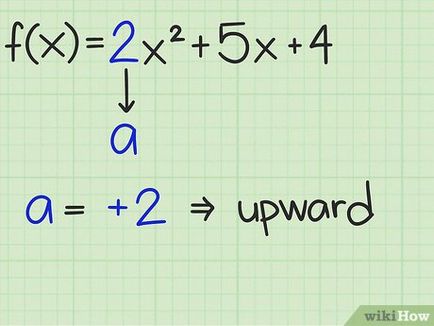
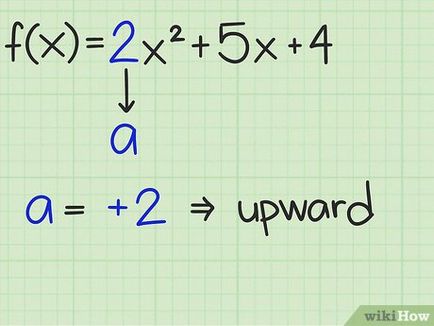
• f (x) = 2 x 4 + 2 x - 6 + 4x-6>. Itt, a = 2. így a parabola felfelé.
• f (x) = - x 3 x 2 + 2 + 8 + 2x + 8>. Itt a = - 3. így a parabola lefelé.
• f (x) = x 2 + 6 +6>. Itt, a = 1. így a parabola felfelé.
• Ha a parabola felfelé irányul, hogy keresni neki legalább. Ha a parabola lefelé irányul, keresi a maximumot.

Kap a megfelelő érték f (x). Helyettesítő talált értéke «x» a kezdeti funkció, hogy megtalálja a megfelelő érték f (x). Így talál minimum vagy maximum funkciót.

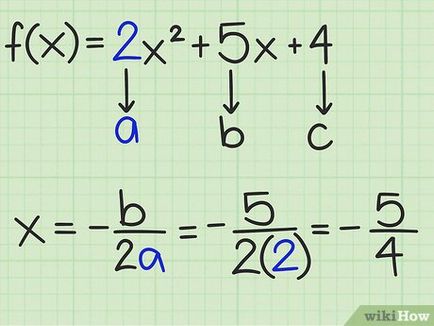
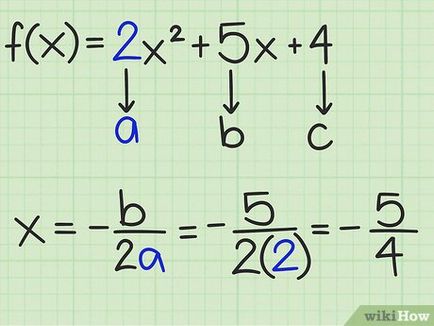
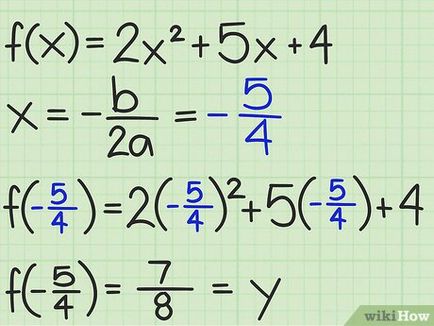
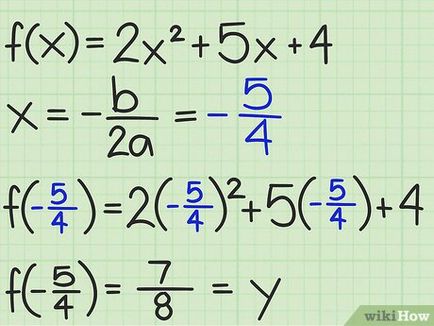
• Az első példában, f (x) = x 2 + 10 x - 1 + 10x-1> akkor kiszámították, hogy a koordináta az "x" a parabola x csúcs = - 5. Az eredeti funkció x helyettesítő - 5. hogy megtalálja a maximális érték:
  • f (x) = x 2 + 10 x - 1 + 10x-1>
  • f (x) = (- 5) 2 + 10 (- 5) - 1 10 (5) -1>
  • f (x) = 25 - 50-1
  • f (x) = - 26
• A második példában, f (x) = - x 3 2 + 6 x - 4 + 6x-4> úgy találja, hogy a koordináta az "x" a parabola csúcsa az x = 1. Az eredeti funkció x helyettesítő 1. hogy megtalálja a maximális érték:
  • f (x) = - x 3 2 + 6 x - 4 + 6x-4>
  • f (x) = - 3 (1) 2 + 6 (1) - 4 6 (1) -4>
  • f (x) = - 3 6 + - 4
  • f (x) = - 1

Írja le a választ. Olvassa újra a nyilatkozatot a problémát. Ha meg kell találni a koordinátákat a csúcsa a parabola, a válasz rekord mindkét érték az x és y (vagy f (x)). Ha azt szeretnénk, hogy kiszámítja a maximális vagy minimális a funkciót, válaszul a felvételen csak az y értékét (vagy f (x)). Ismét, nézd meg a jele az együttható a. hogy ellenőrizze, hogy számított: a maximális vagy minimális.

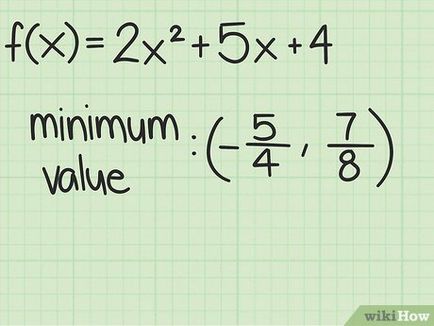
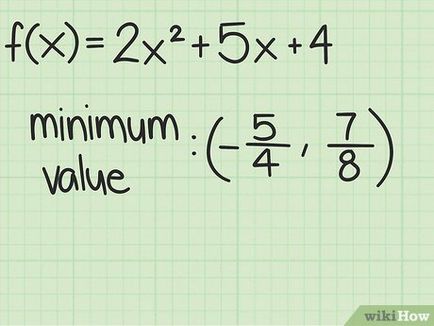
• Az első példában, f (x) = x 2 + 10 x - 1 + 10x-1> egy pozitív érték, úgy, hogy a számított legkisebb. parabola csúcsa fekszik a koordináták (- 5 - 26). és a minimális értékét a függvény egyenlő - 26.
• A második példában, f (x) = - x 3 2 + 6 x - 4 + 6x-4> negatív érték, így megtalálni a maximális. parabola csúcsa fekszik koordinátáit (1 - 1). és a maximális értéket a függvény egyenlő - 1.