Hogyan lehet megtalálni a hossza az oldalán a háromszög

több szegmensre osztható tetszőleges háromszög, amelynek hossza van kiszámításához szükséges a leggyakrabban. Ezek a szegmensek összekötő ponton, amely a háromszög-csúcsot a központok az oldalán, a központok a beírt és körülírt körök, hanem más fontos pont a háromszög geometria. Egyes kiviteli alakokban kiszámítja a hossza az ilyen szegmensek az euklideszi geometria az alábbiakban mutatjuk be.

Ha a szegmens szeretne keresni, akkor csatlakozik bármely két csúcsa olyan háromszög, az egyik oldalán a geometriai alakzat. Ha ismert, például, a hossza a másik két oldal (A és B) és az a szög, amely képeznek (γ), a hossza ebben a szegmensben (C), akkor lehet számolni, amely a koszinusz tétel. Fold a négyzetei oldalainak hossza, kivonás eredményét a két oldala azonos hosszúságú, szorozva a koszinusza a szög formában, és akkor kap a négyzetgyöke az eredő érték: C = √ (a² + b²-2 * A * B * cos (γ)).

Ha egy sor egyikénél indul a csúcsai a háromszög, végül a másik oldalon, és a rá merőleges, akkor ez a szegmens az úgynevezett magasság (h). Megtalálható, például, ismerve a terület (ek), és a hossza (A) az oldal, amelyre a magasságot csökkentjük - ossza területének kétszerese az oldal hosszát: h = 2 * S / A.

Ha a szegmens összekötő a közepén mindkét oldalán olyan háromszög felső és szemben fekvő ezen az oldalon, a neve ebben a szegmensben a medián (m). Megtalálja a hossza lehet, például, ismerve a oldalainak hossza (A, B, C) - szeres megduplázódott négyzetek hosszának két oldalán, a kivonást kapott értéket a tér a oldalon a közepén, amely a végek vágott, és akkor kap a négyzetgyökét egynegyede az eredmény: m = √ ((2 * a² + 2 * b²-C²) / 4).

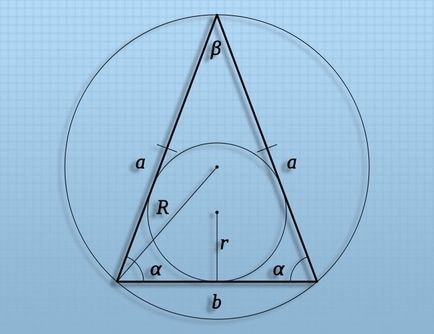
Ha egy összekötő vonal közepén a beírt kör egy tetszőleges háromszög, és minden kör érintési pontok az oldalán a háromszög, majd keresse meg a hosszát, hogy kiszámítjuk a sugár (r) a beírt kör. Erre a célra, például, felosztják a területet (S) a háromszög, a kerülete mentén (P): r = S / P.

Ha egy összekötő vonal közepén a köré rajzolt kör körülbelül egy tetszőleges háromszög, bármely a csúcsai a figura, a hossza lehet kiszámítani találni a sugara a körülírt kör (R). Ha ismert, például, a hossza az egyik oldalon (A) egy háromszög és az a szög (α), szemben fekvő ez, hogy ki lehessen számítani a hossza a kívánt intervallum, felosztják a hossza a részt kétszer sine a szög: R = A / (2 * sin (α )).

Annak érdekében, hogy megtanulják az összes oldalán a háromszög, meg kell tudni, hogy a szög és a két szomszédos láb, vagy az érték két szög és az oldalsó közöttük. Ha tudja, hogy a szögek a háromszög, majd keresse meg a hossza minden oldalán egy háromszög lehetetlen, de megtalálható az arány a háromszög oldalainak.

Az első esetben az ilyen adatok ismertek a háromszög a nagysága a szög és a hossza a lábak alkotják a szöget. A szemközti oldalon az ismert szög, az szükséges, hogy megtaláljuk a koszinusztétel, amely szerint a szükséges hosszát az ismert felek négyzetének és hajtogatott, majd kivonjuk a vett összege termék ezen oldala, két és megszorozzuk a koszinusz a szög formájában.
A képlet E számítás a következő:

h = √ (e2 + f2 - 2ef * cosa), ahol:

e és f - ismert hossza a lábak;

h - az ismeretlen láb (vagy párt);

A - szögben, amelyet a lábak ismert.

A második esetben, amikor tudod, hogy a két szög és a lábát a háromszög között, meg kell használni a tétel a szinusz. Szerint ez a tétel, ha a szinusz a szög osztva a hossza a másik lábát, akkor kap egy arányban, minden más ebben a háromszögben. Továbbá, ha nem tudja a jobb lábát, könnyen talál, tudva azt, hogy a háromszög szögei egyenlő összegű Stam és nyolcvan fokban.
Ez a kijelentés lehet írni, mint egy képlet:

Sind / d = Sinf / f = szinusz / e, ahol:

D, F, E - értéke szemközti szöge;

d, f, e - a lábak, megfelelő, egymással szemben sarkok.

A harmadik esetben, amelyről csak a sarkokat a háromszög, így nem lehet tudni, hogy a hossza minden oldalán a háromszög. De megtalálja a hozzáállása ezek a pártok és a kiválasztási módszer találni egy hasonló háromszöget. Az arány az oldalán a háromszög megtalálható kidolgozásával rendszer három egyenlet három ismeretlennel.
Íme a képlet összeállításához:

d, f, e - ismeretlen lábak a háromszög;

D, F, E - a szögek ellenkező befogó ismeretlen.