A méret alapján vektortér és
Amikor megvitattuk a fogalmát n-dimenziós vektorba és bevihetjük művelet vektorokba, azt találtuk, hogy a készlet minden n-dimenziós vektorok generál lineáris tér. Ebben a cikkben fogunk beszélni a legfontosabb kapcsolódó fogalmak - a dimenziót, és alapja a vektortér. Is, úgy az elmélet a bomlási egy tetszőleges vektor alapján, és kapcsolatot a különböző bázisok n-dimenziós térben. Elemezzük részletesen konkrét példákat megoldásokat.
Oldalnavigáció.
A koncepció egy vektortér dimenziója és alapja.
A méret vektortér a szám egyenlő a maximális számú lineárisan független vektorok ebben a térben.
Alapján vektortér - rendezett halmaza lineárisan független vektorok ebben a térben, melyek száma megegyezik a dimenzió a tér.
Íme néhány megfontolások alapján ezek a meghatározások.
Tekintsük a tér n-dimenziós vektorok.
Megmutatjuk, hogy a dimenziója ennek teret egyenlő n.
Vegyünk egy rendszer n egység vektorok formájában
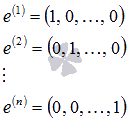
Tegyük fel, ezek a vektorok, mint mátrix sorai a A. Ebben az esetben, az A mátrix egy egységnyi mátrix dimenzió n és n. A rangsorban a ez a mátrix egyenlő n-nel (ha szükséges, lásd a cikk rang mátrix: meghatározzuk, találni technikák). Következésképpen, a rendszer a vektorok lineárisan független, és ez a rendszer nem tudja hozzáadni egy vektor megsértése nélkül lineáris függetlenségét. Mivel a vektorok számát a rendszerben egyenlő n-nel. dimenziója a tér n-dimenziós vektorok értékét visszaállítja az n. és az egység vektorok alapot ezt a helyet.
Az utolsó állítás és meghatározása alapján arra lehet következtetni, hogy a rendszer n-dimenziós vektorok, a vektorok számát, amelyekben n-nél kisebb. Ez nem egy alapon.
Most cserélni az első és a második vektor rendszer. Könnyen azt mutatják, hogy a kapott vektor rendszer is alapja az n-dimenziós vektortér. Összetétele a mátrix, figyelembe annak sorvektorait ennek a rendszernek. Ez a mátrix lehet származik az identitás mátrix kicserélésével az első és második sor, így annak rang egyenlő n-nel. Így a rendszer n lineárisan független vektor és egy alapon n dimenziós vektortér.
Ha cserélni a más vektorok a rendszer, azt látjuk, a másik alapján.
Ha veszel egy lineárisan független rendszer nem egység vektorok, ez is az alapja az n-dimenziós vektortér.
Tehát a vektor tér n dimenziós annyi bázis, ahány lineárisan független rendszer n n-dimenziós vektorok.
Ha beszélünk a két-dimenziós vektortér (azaz a gépen), annak alapján bármely két nem kollineáris vektor. Alapján háromdimenziós tér bármely három nem egy síkba eső vektorok.
Tekintsük néhány példát.
Vannak a vektorok alapján három-dimenziós vektortér?
A bomlás vektorok alapján vektortér.
Legyen tetszőleges vektorok alapján n-dimenziós vektortér. Ha ehhez hozzátesszük, hogy ez egy n-dimenziós vektor x. A kapott rendszer vektorok lineárisan függ. tudjuk, hogy legalább egy vektor lineárisan függ a rendszer van kifejezve a másik lineáris lineáris összefüggés a tulajdonságait. Más szóval, legalább az egyik a vektorok lineárisan függ a rendszer bontja a maradék vektorok.
Ez elvezet minket egy nagyon fontos tétel.
Bármely olyan vektor, n dimenziós vektortér egyedileg elbomlik alapján.
Hagyja - alapján az n-dimenziós vektortér. Mi hozzá, hogy ezek a vektorok n-dimenziós x vektor. Ezután a kapott rendszer vektorok lineárisan függ, és a vektor x kifejezhető lineárisan szempontjából vektorok, ahol a - néhány számot. Tehát kaptunk bővülése x alapján. Továbbra is azt bizonyítják, hogy ez a bomlás egyedülálló.
Tegyük fel, hogy van egy másik bomlás, ahol - néhány számot. Vonjuk a bal és jobb oldalán az utolsó egyenlőség, illetve a bal és a jobb oldalon az egyenlet:
Mivel a rendszer alap vektorok lineárisan függetlenek, akkor definíció szerint a lineáris függetlenség vektorok kapott egyenlőség csak akkor lehetséges, ha minden együttható nulla. Ezért mi azt bizonyítja egyediségét bomlás vektor alapján.
Az együtthatókat az úgynevezett koordinátáit x alapján.
Miután megismerése a tétel a bomlás a vektor alapján, elkezdjük megérteni a lényegét az „nekünk adott egy n-dimenziós vektor.” Ez a kifejezés azt jelenti, hogy figyelembe vesszük a x vektor n-dimenziós vektortér, amelynek koordinátáit kapnak egy bizonyos alapot. Ugyanakkor tudjuk, hogy ugyanaz a vektor x másik alapja az n-dimenziós vektortér lesz koordinátákat, amelyek eltérnek.
Tekintsük a következő problémát.
Tegyük fel, hogy bizonyos alapján n-dimenziós vektortér adott egy rendszer n lineárisan független vektor
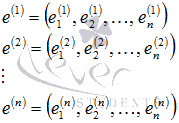
és a vektor. Ezután a vektorok szintén ennek alapján vektortér.
Tegyük fel, hogy szeretné megtalálni a koordinátái x vektor az alapon. Jelöljük ezeket a koordinátákat hasonlók.
A vektor x alapján ábrázolás. Írunk ez az egyenlet a koordináta formájában:
Ez az egyenlet egyenértékű rendszer n lineáris egyenletek n ismeretlen változó:
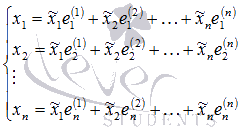
Összefoglalás A mátrix rendszer formájában
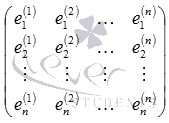
Jelöljük a levél A. A mátrix oszlopai lineárisan független vektor vektorok, úgy, hogy a rangot ez a mátrix egyenlő n-nel. ezért determináns nulla. Ez a tény azt jelzi, hogy a rendszer egy egyedi megoldás, amely megtalálható bármilyen módszerrel, például úgy, hogy Kramer vagy mátrix módszer.
Mivel a kívánt koordinátáit x alapján megtalálhatók lesznek.
Nézzük az elmélet példákkal.
Az alapot egy három-dimenziós vektortér adott vektorok
Győződjön meg arról, hogy a rendszer a vektorok is alapja ennek a térnek, és megtalálja a koordinátákat a vektor x ezen az alapon.
A vektor rendszer alapján három-dimenziós vektortér azért van szükség, hogy lineárisan független. Hadd magyarázzuk ezt meghatározásával rangot A. sorok vektorok. Ligában talál Gauss módszer
Ezért, Rank (A) = 3. azt mutatja, hogy lineáris függetlenség vektorok.
Tehát az alap vektorok. Legyen ez alapján x vektor koordinátái. Aztán, ahogy azt korábban bemutattuk, a kapcsolat koordinátái által meghatározott a vektor egyenletrendszer
Lecserélésére ismert állapot értékeket kapjuk, hogy
Mi megoldjuk Kramer:

Tehát a vektor x van egy alapja koordinátákat.
.