Teljesítmény funkció, tulajdonságai és grafikonok

Tulajdonságok hatalmi funkciók és grafikonok

Ezután vesszük a hatványfüggvény
y (x) = x p.

A teljesítmény függvényt egy kitevővel egyenlő nulla, p = 0

Ha a kitevő a hatványfüggvény y = x p értéke nulla, p = 0. a hálózati funkció határozza meg az összes x ≠ 0, és állandó egyenlő egységét:






y = x p = x 0 = 1, x ≠ 0.

A teljesítmény függvényt egy természetes páratlan exponens, p = n = 1, 3, 5.

Tekintsük a teljesítmény függvényt y = xp = xn természetes páratlan n kitevő = 1, 3, 5. Ez az összetevő is írható: n = 2k + 1, ahol k = 0, 1, 2, 3. - nem negatív egész szám . Az alábbiakban a tulajdonságait és grafikonok az ilyen funkciókat.

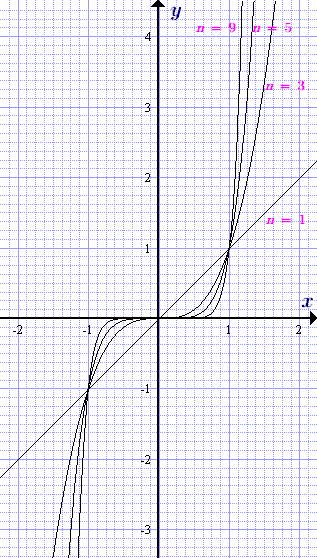
Ütemezése a teljesítmény függvényt y = x n természetes páratlan indexű különböző értékeire a kitevő n = 1, 3, 5.

A domain a meghatározás: -∞ Az értékrend: -∞ Parity: páratlan, y (-x) = - y (x)
Monotónia: monoton
Szélsőséges: nincs
konvexitási:
a -∞ 0 Az inflexiós pont: x = 0, y = 0
A metszéspontjai a koordinátatengelyek x = 0, y = 0
határértékek:
;
Egyéni értékek:
ha x = -1,
y (-1) = (-1) n ≡ (-1) 2k + 1 = -1
ha x = 0, y (0) = 0, n = 0
ha x = 1, y (1) = 1, n = 1
Kapcsolat funkció:
ha n = 1 funkció inverzét magának: x = y
ha n ≠ 1. gyökér inverz függvényeként fokú n.

A teljesítmény függvényt egy természetes páratlan exponens, p = n = 2, 4, 6.

Tekintsük a teljesítmény függvényt y = x p = x n, még a természetes n kitevő = 2, 4, 6. Egy ilyen indikátor is írt, mint: n = 2k. ahol k = 1, 2, 3. - pozitív. Tulajdonságok és grafikonok ezeket a funkciókat az alábbiakban közöljük.

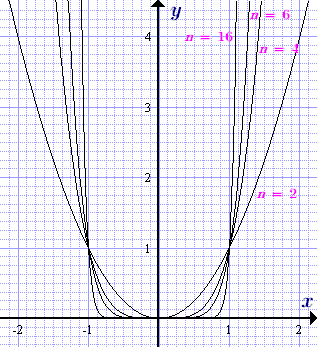
Ütemezése a teljesítmény függvényt y = x n természetes kitevővel akkor is, ha különböző értékeit a kitevő n = 2, 4, 6.

A domain a meghatározás: -∞ A beállított értékek: 0 ≤ y <∞
Parity: egyenletes, y (-x) = y (x)
monotónia:
x <0 монотонно убывает
ha x> 0 monoton növekszik
Szélsőséges: minimális, X = 0, y = 0
Konvexitási: domború lefelé
Az inflexiós pont: nincs
A metszéspontjai a koordinátatengelyek x = 0, y = 0
határértékek:
;
Egyéni értékek:
ha x = -1. y (-1) = (-1) n ≡ (-1) 2k = 1
ha x = 0, y (0) = 0, n = 0
ha x = 1, y (1) = 1, n = 1
Kapcsolat funkció:
ha n = 2 négyzetgyöke:
ha n ≠ 2. gyökere n.

A teljesítmény függvényt negatív kitevő, p = n = -1, -2, -3.

Tekintsük a teljesítmény függvényt y = x p = x n negatív n kitevő = -1, -2, -3. Ha teszünk n = -k. ahol k = 1, 2, 3 - természetes, ez úgy reprezentálható, mint:

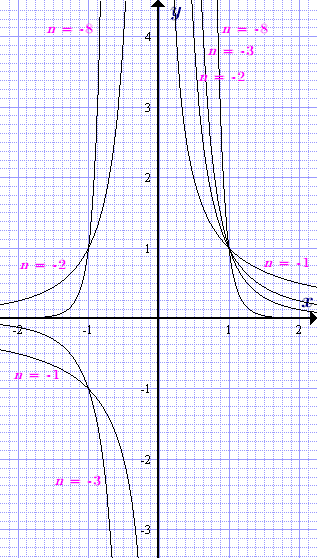
Ütemezése a teljesítmény függvényt y = x n egy negatív index különböző értékeire a kitevő n = -1, -2, -3.

Páratlan index, n = -1, -3, -5.

Az alábbiakban a tulajdonságok a függvény az y = x n páratlan negatív index n = -1, -3, -5.

meghatározzuk TERÜLET: x ≠ 0
A beállított értékek: y ≠ 0
Parity: páratlan, y (-x) = - y (x)
Monotónia: monoton csökken
Szélsőséges: nincs
konvexitási:
x <0. выпукла вверх
ha x> 0. konvex lefelé
Az inflexiós pont: nincs
A metszéspontok a koordináta tengelyekkel: nincs
jel:
x <0, y <0
ha x> 0, y> 0
határértékek:
; ; ;
Egyéni értékek:
ha x = -1, y (-1) = (-1) n = -1
ha x = 1, y (1) = 1, n = 1
Kapcsolat funkció:
ha n = -1.
n <–2.

Még index, n = -2, -4, -6.

Az alábbiakban a tulajdonságok a függvény az y = x n még negatív index n = -2, -4, -6.

meghatározzuk TERÜLET: x ≠ 0
A beállított értékek: y> 0
Parity: egyenletes, y (-x) = y (x)
monotónia:
x <0. монотонно возрастает
ha x> 0. monoton csökken
Szélsőséges: nincs
Konvexitási: domború lefelé
Az inflexiós pont: nincs
A metszéspontok a koordináta tengelyekkel: nincs
Jelzés: y> 0
határértékek:
; ; ;
Egyéni értékek:
ha x = -1, y (-1) = (-1) n = 1
ha x = 1, y (1) = 1, n = 1
Kapcsolat funkció:
ha n = -2.
n <–2.

Teljesítmény funkció racionális (tört) kijelző

Tekintsük a teljesítmény függvényt y = x p racionális (frakcionált) kitevő. ahol n - egy egész szám, m> 1 - pozitív. Amely képletben n, m nincs közös osztója van.

A nevező a frakcionált index - páratlan

Tegyük fel, hogy a nevező a frakcionált exponens páratlan: m = 3, 5, 7. Ebben az esetben, egy teljesítmény x p funkció határozza egyaránt pozitív és negatív értékek az x argumentumot. Tekintsük tulajdonságok, mint az exponenciális függvények, ahol index p egy bizonyos tartományon belül.

Ez negatív p, p <0

Legyen racionális exponens (páratlan nevező m = 3, 5, 7) kisebb, mint nulla.

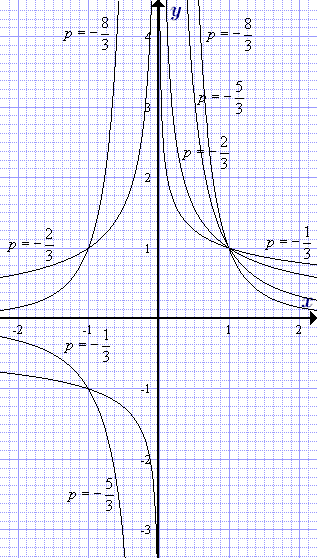
Grafikonok exponenciális függvények negatív fénytörési racionális különböző értékei esetén a kitevő. ahol m = 3, 5, 7 - páratlan.

Páratlan számlálóban, n = -1, -3, -5.

Itt vannak a tulajdonságai a hálózati funkció y = x p racionális negatív index. ahol n = -1, -3, -5. - negatív páratlan szám, m = 3, 5, 7 - páratlan egész szám.

meghatározzuk TERÜLET: x ≠ 0
A beállított értékek: y ≠ 0
Parity: páratlan, y (-x) = - y (x)
Monotónia: monoton csökken
Szélsőséges: nincs
konvexitási:
x <0. выпукла вверх
ha x> 0. konvex lefelé
Az inflexiós pont: nincs
A metszéspontok a koordináta tengelyekkel: nincs
jel:
x <0, y <0
ha x> 0, y> 0
határértékek:
; ; ;
Egyéni értékek:
ha x = -1, y (-1) = (-1) n = -1
ha x = 1, y (1) = 1, n = 1
Kapcsolat funkció:

Még számlálóban, n = -2, -4, -6.

Tulajdonságai a hálózati funkció y = x p racionális negatív index. ahol n = -2, -4, -6. - akár negatív egész szám, m = 3, 5, 7 - páratlan egész szám.

meghatározzuk TERÜLET: x ≠ 0
A beállított értékek: y> 0
Parity: egyenletes, y (-x) = y (x)
monotónia:
x <0. монотонно возрастает
ha x> 0. monoton csökken
Szélsőséges: nincs
Konvexitási: domború lefelé
Az inflexiós pont: nincs
A metszéspontok a koordináta tengelyekkel: nincs
Jelzés: y> 0
határértékek:
; ; ;
Egyéni értékek:
ha x = -1, y (-1) = (-1) n = 1
ha x = 1, y (1) = 1, n = 1
Kapcsolat funkció:

P pozitív arány kevesebb, mint egy, 0

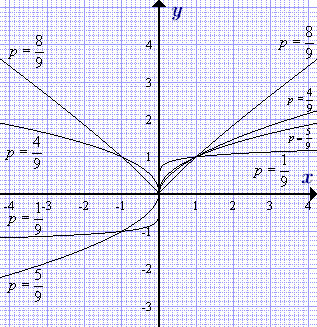
A grafikon a teljesítmény funkció racionális exponens (0

Páratlan számlálóban, n = 1, 3, 5.

A tulajdonságait a hálózati funkció y = x p egy racionális indikátor. Mi vagyunk a 0

A domain a meghatározás: -∞ Az értékrend: -∞ Parity: páratlan, y (-x) = - y (x)
Monotónia: monoton
Szélsőséges: nincs
konvexitási:
x <0. выпукла вниз
ha x> 0. konvex, felfelé irányuló
Az inflexiós pont: x = 0, y = 0
A metszéspontjai a koordinátatengelyek x = 0, y = 0
jel:
x <0, y <0
ha x> 0, y> 0
határértékek:
;
Egyéni értékek:
ha x = -1, y (-1) = -1
ha x = 0, y (0) = 0
ha x = 1, y (1) = 1
Kapcsolat funkció:

Még számlálóban, n = 2, 4, 6.

A tulajdonságait a hálózati funkció y = x p egy racionális indikátor. Mi vagyunk a 0

A domain a meghatározás: -∞ A beállított értékek: 0 ≤ y <+∞
Parity: egyenletes, y (-x) = y (x)
monotónia:
x <0. монотонно убывает
ha x> 0. monoton
Szélsőséges: legalább az x = 0, y = 0
Konvexitási: felfelé konvex, ha x ≠ 0
Az inflexiós pont: nincs
A metszéspontjai a koordinátatengelyek x = 0, y = 0
Regisztráció: ha x ≠ 0, y> 0
határértékek:
;
Egyéni értékek:
ha x = -1, y (-1) = 1
ha x = 0, y (0) = 0
ha x = 1, y (1) = 1
Kapcsolat funkció:

Exponent p értéke nagyobb, mint egy, p> 1

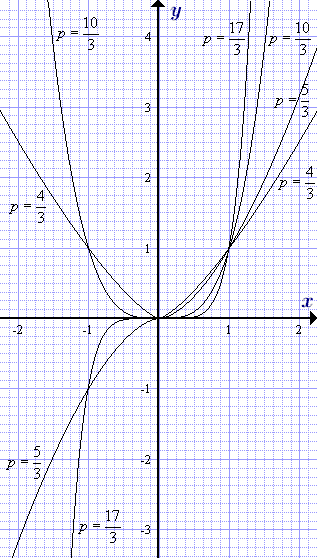
Ütemezése hatványfüggvénnyel egy racionális indikátor (p> 1) különböző értékeket a kitevő. ahol m = 3, 5, 7 - páratlan.

Páratlan számlálóban, n = 5, 7, 9.

Tulajdonságok A hatványfüggvény y = x p racionális kitevő nagyobb, mint egy. Ahol n = 5, 7, 9 - páratlan egész szám, m = 3, 5, 7 - páratlan egész szám.

A domain a meghatározás: -∞ Az értékrend: -∞ Parity: páratlan, y (-x) = - y (x)
Monotónia: monoton
Szélsőséges: nincs
konvexitási:
a -∞ 0 Az inflexiós pont: x = 0, y = 0
A metszéspontjai a koordinátatengelyek x = 0, y = 0
határértékek:
;
Egyéni értékek:
ha x = -1, y (-1) = -1
ha x = 0, y (0) = 0
ha x = 1, y (1) = 1
Kapcsolat funkció:

Még számlálóban, n = 4, 6, 8.

Tulajdonságok A hatványfüggvény y = x p racionális kitevő nagyobb, mint egy. Ahol N = 4, 6, 8 - páros egész, m = 3, 5, 7 - páratlan egész szám.

A domain a meghatározás: -∞ A beállított értékek: 0 ≤ y <∞
Parity: egyenletes, y (-x) = y (x)
monotónia:
x <0 монотонно убывает
ha x> 0 monoton növekszik
Szélsőséges: legalább az x = 0, y = 0
Konvexitási: domború lefelé
Az inflexiós pont: nincs
A metszéspontjai a koordinátatengelyek x = 0, y = 0
határértékek:
;
Egyéni értékek:
ha x = -1, y (-1) = 1
ha x = 0, y (0) = 0
ha x = 1, y (1) = 1
Kapcsolat funkció:

A nevező a frakcionált index - még

Tegyük fel, hogy a frakcionált nevező az exponens még: m = 2, 4, 6. Ebben az esetben az X o teljesítmény függvényt nincs definiálva a negatív értékek az érvelés. A tulajdonságai azonosak a tulajdonságai a hálózati funkció exponens irracionális (lásd. A következő szakaszban).

Teljesítmény funkció irracionális kitevő

Tekintsük a teljesítmény függvényt y = x p irracionális kitevő p. Az olyan tulajdonságok, funkciók eltérnek a fent abban, hogy nincsenek meghatározva a negatív értékek az érvelés x. A pozitív értékek az érvelés, a tulajdonságok csak attól függ a kitevő értéke p, és nem függ attól, hogy p jelentése egy egész szám, racionális vagy irracionális.

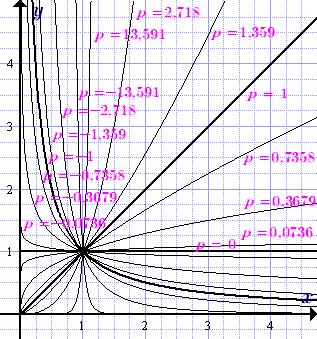
Ütemezése a teljesítmény függvényt y = x p irracionális mutató különböző értékeire a kitevő p.

Teljesítmény funkció negatív kitevő p <0

meghatározzuk TERÜLET: x> 0
A beállított értékek: y> 0
Monotónia: monoton csökken
Konvexitási: domború lefelé
Az inflexiós pont: nincs
A metszéspontok a koordináta tengelyekkel: nincs
Korlátok :;
Konnotáció: Amikor x = 1, y (1) = 1, p = 1

Hatványfüggvény pozitív kitevő p> 0

Index kevesebb, mint egy 0

meghatározzuk TERÜLET: x ≥ 0
A beállított értékek: y ≥ 0
Monotónia: monoton
Konvexitási: konvex, felfelé irányuló
Az inflexiós pont: nincs
A metszéspontjai a koordinátatengelyek x = 0, y = 0
határértékek:
Magán jelentése: amennyiben x = 0, y (0) = 0 p = 0.
Amikor X = 1, y (1) = 1, p = 1

Sebessége nagyobb, mint egy p> 1

meghatározzuk TERÜLET: x ≥ 0
A beállított értékek: y ≥ 0
Monotónia: monoton
Konvexitási: domború lefelé
Az inflexiós pont: nincs
A metszéspontjai a koordinátatengelyek x = 0, y = 0
határértékek:
Magán jelentése: amennyiben x = 0, y (0) = 0 p = 0.
Amikor X = 1, y (1) = 1, p = 1