számsor
1. Alapvető fogalmak
Hagyja, U1, U2. U3. ..., un. ... végtelen számsorozat. kifejezés
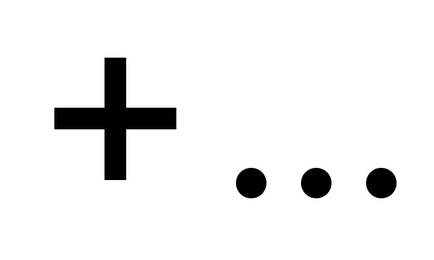
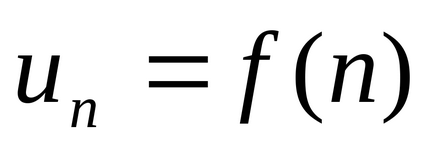
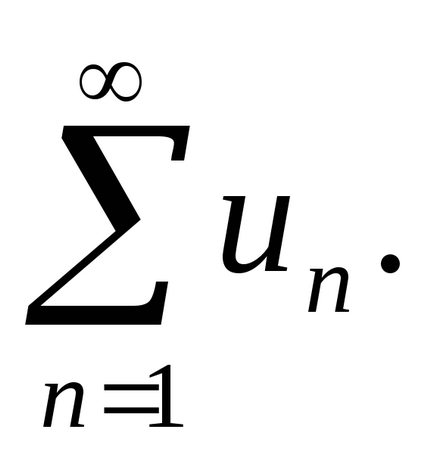
A összege az első n tagjai egy számsorozat jelöljük
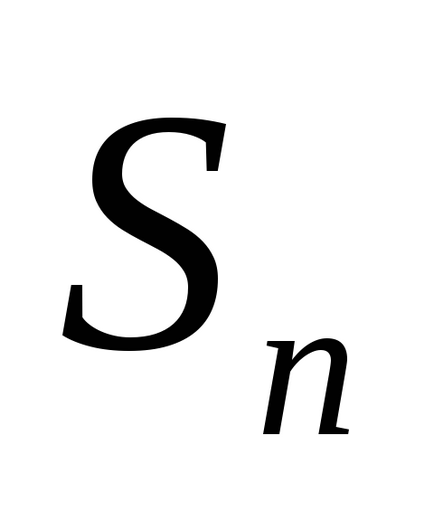
.
Sorozat nevezik konvergens. ha az n-edik részösszegként
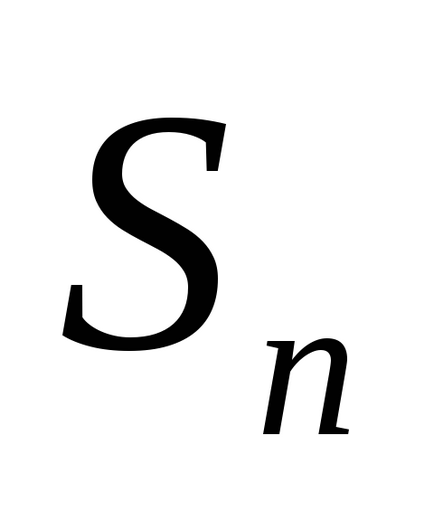
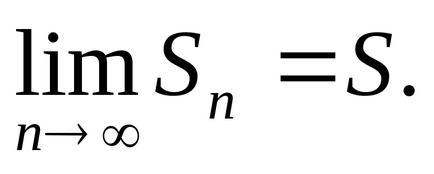

Ha az n-edik részösszegként a sorozat
1. példa Keresse meg az összeget a sorozat.
Határozat. van
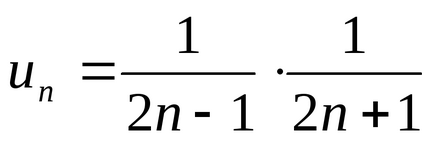
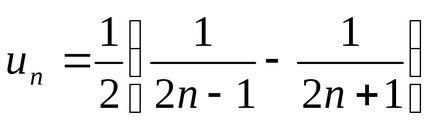
.
Azóta a sorozat konvergál és összege
2. A fő tételek a numerikus sorozat
Tétel 1. Ha a sorozat


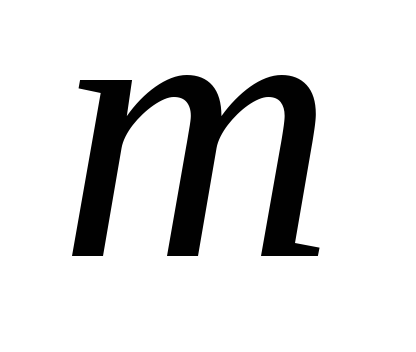
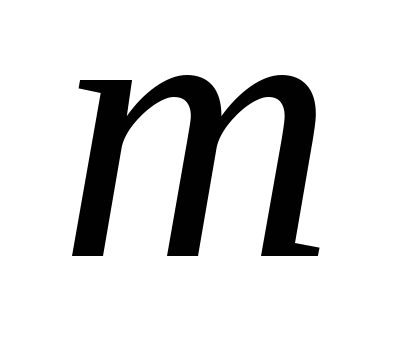
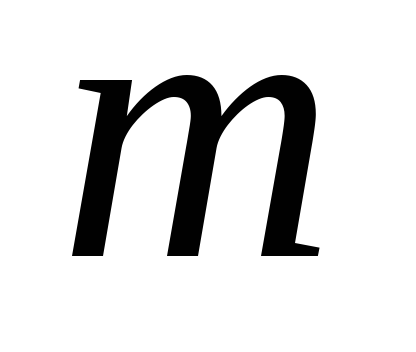
2. tétel Ha a sorozat, és ez az összeg a számát

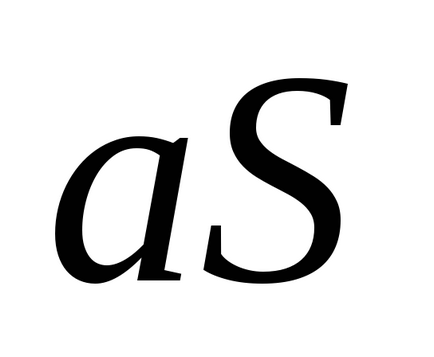
3. tétel Ha egyetért sorok rendre summyS és Q, a sorozat konvergál, és az összeg egyenlő az utolsó sor
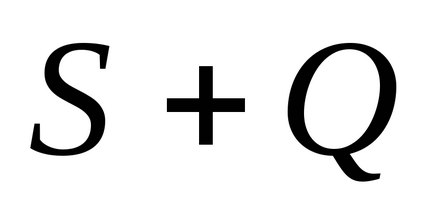
Tétel 4 (a szükséges a konvergencia a sorozat). Ha a sorozat konvergál,
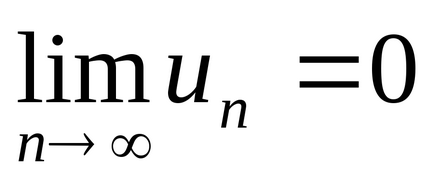
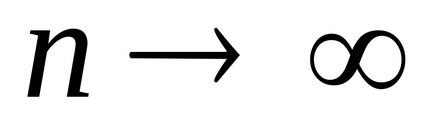
Következmény 1. Ha
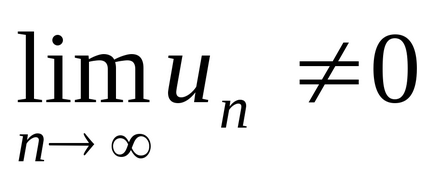
2. Következmény Ha
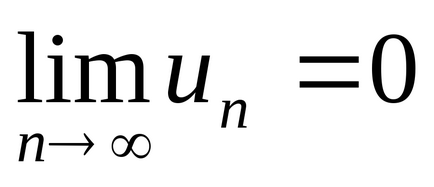
2. példa Vizsgáljuk a konvergencia sorozat:
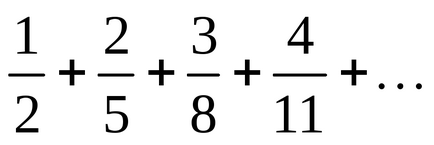
Határozat. Keresse az általános kifejezés a sorozat. Mivel:
,
azaz
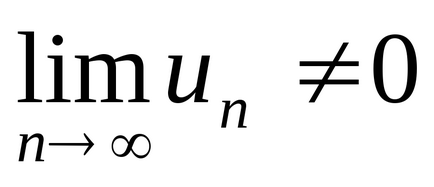
3. jelei konvergencia sorozat pozitív értelemben
3.1. közvetlen összehasonlító teszt
Közvetlen összehasonlító teszt összehasonlításán alapul egy előre meghatározott számú konvergencia számos divergenciája vagy konvergenciája amely ismert. Összehasonlításképpen, az itt felsorolt sorozat.
sor
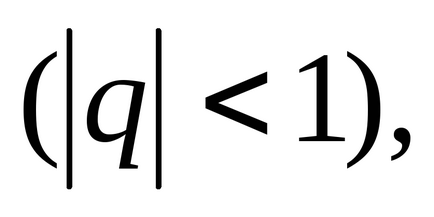
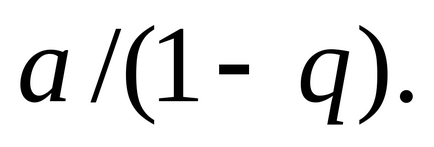
sor
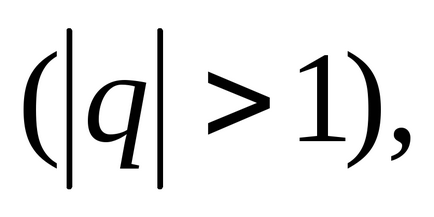
sor
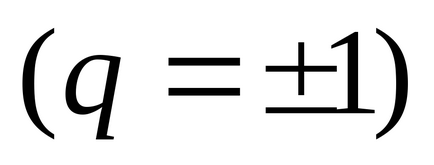
Sorozat nevezzük Dirichlet sor. Pri> 1 Dirichlet sorozat konvergál <1- расходится.
Amikor = 1 sorozat
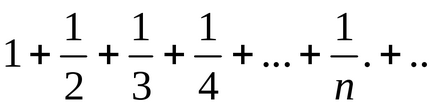
Tétel. Az első jele az összehasonlítás. két sorozat pozitív értelemben Tegyük fel, hogy:
ahol minden egyes tagja a sorozat (1) nem haladja meg a megfelelő tagok száma (2), azaz a
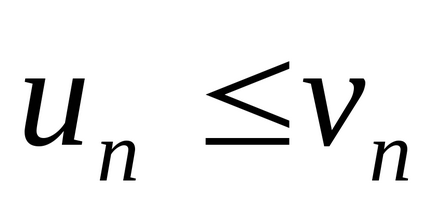
Megjegyzés. Ez a funkció továbbra is érvényben ha neravenstvo
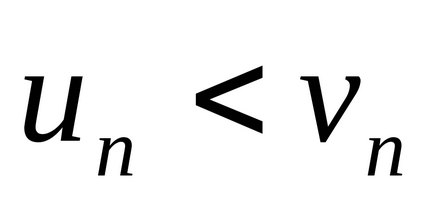
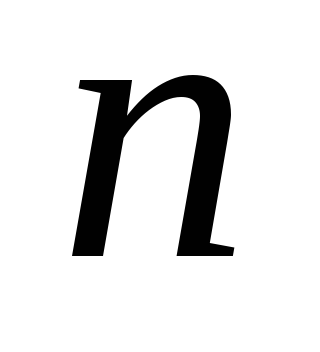

3. példa Annak vizsgálatára, a konvergencia
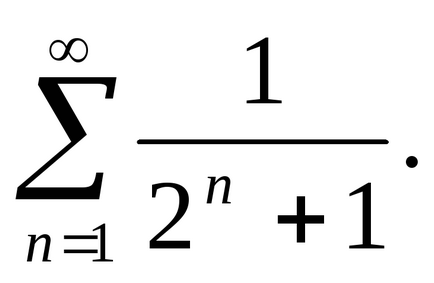
Határozat. A tagok a sorozat kisebb, mint a megfelelő feltételeket a sorozat
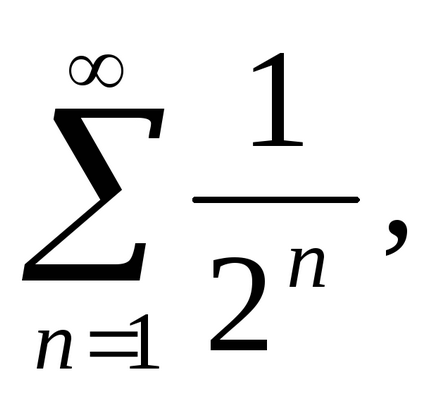
Tétel. A második funkció összehasonlító (összehasonlító vizsgálat korlátozó formában). Ha van egy véges és nem nulla határérték
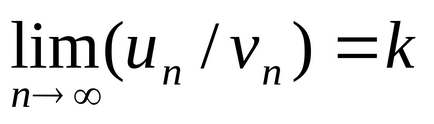
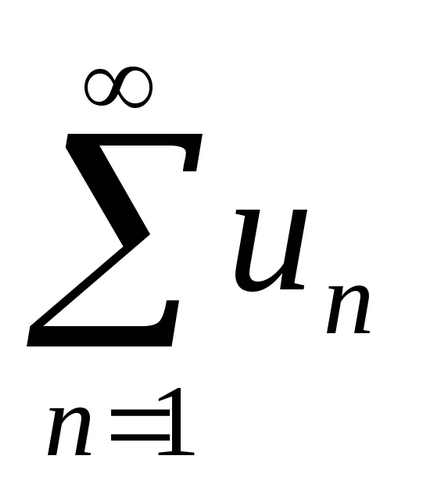
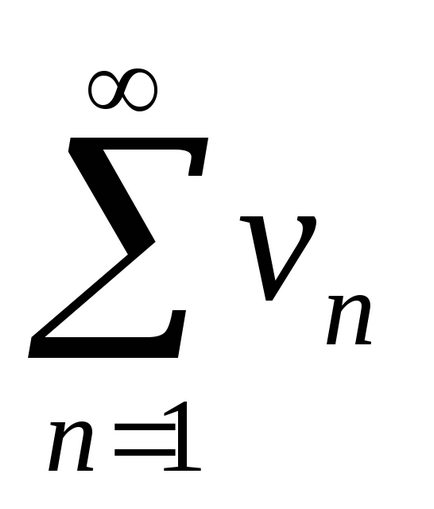
4. példa Annak vizsgálatára, a konvergencia
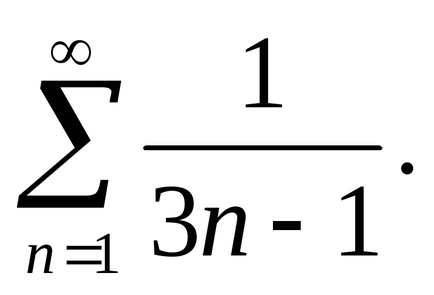
Határozat. Összehasonlítható a szám a harmonikus sor
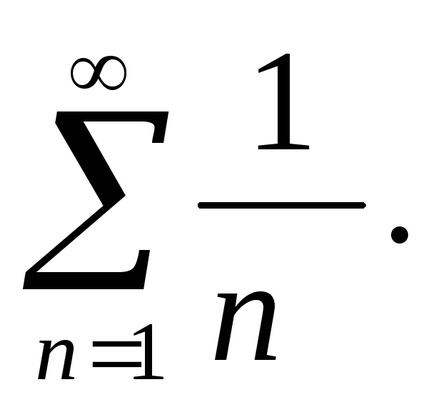
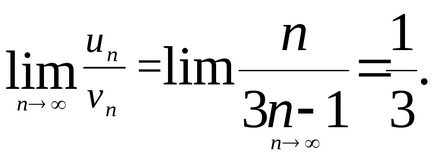
Mivel a harmonikus sor divergens, akkor eltér, és kap egy számot.