Rugalmas és rugalmatlan ütközések fizika

A törvény a mechanikai energia megmaradás és a törvény lendületmegmaradás megoldást találni, hogy mechanikai problémák, amennyiben az eljáró erők ismeretlen. Egy példa az ilyen problémák hatással van a kölcsönhatás a szervek.

Kölcsönhatás sokk szervek gyakran kell foglalkozni a mindennapi életben, a művészet és a fizika (különösen a fizika atom és az elemi részecskék).

A stroke (vagy ütközés) nevezik átmeneti kölcsönhatása szervek, amelynek eredményeként a sebesség jelentős változásokon megy keresztül. Abban az időben a hatása köztük rövid sokk erők, amelyek értéke általában ismeretlen. Ezért a kalapács nem látható közvetlenül kölcsönhatása Newton törvényei. Jogszabályok alkalmazásának az energiamegmaradás és a lendület, sok esetben, hogy megszüntesse a megfontolásból az ütközési folyamat maga, és kap a kapcsolatát sebesség szervek előtt és után ütközés, megkerülve minden közbenső értéket ezeket a mennyiségeket.

A szerelők gyakran két modell sokk kölcsönhatás - teljesen rugalmas és teljesen rugalmatlan ütközés.

Udaromnazyvayut teljesen rugalmatlan hatása kölcsönhatásra, amelyben az egyesített test (coalesce) egymással és lépni, mint egy test.

Amikor teljesen rugalmatlan ütközés mechanikai energiát nem konzervált. Ez részben vagy teljesen átalakul belső energiája a testek (fűtés).

Egy példa egy teljesen rugalmatlan hatása szolgálhat golyók hit (vagy shell) egy ballisztikus inga. Az inga egy doboz homoktömegben M. felfüggesztett kötelek (ábra. 1.21.1). Bullet m tömeget. repülő vízszintesen hiányzik a dobozból, és beragadt ott. Az elhajlás az inga lehet meghatározni a sebességet egy golyó.

Jelöljük sebesség doboz elakadt golyó, időben a törvény szerint a lendületmegmaradás

Dzsemek golyók a homokban veszteség volt mechanikai energia:

Az arány M / (M + m) - aránya a kinetikus energia a lövedék, amely átesett a belső energia a rendszer:

Ez a képlet alkalmazható nemcsak a ballisztikus inga, hanem bármely rugalmatlan ütközés két test különböző tömegeket.

szinte az összes kinetikus energiája golyó bejut a belső energia. Amikor m = M

a belső energia válik fele a kezdeti kinetikus energia. Végül, egy rugalmatlan ütközés a mozgó test egy nagy tömegű rögzített test kis tömegű (m >> M) arányt

További mozgása az inga segítségével számítható a törvény mechanikai energia megmaradás:

ahol h - a maximális magassága az inga emelés. Ezekből kapcsolataiért alábbiak szerint:

Magasságának mérésével h tapasztalatai alapján az inga lift, akkor meg a sebességet a golyó v.

Általában a tömeges m1 és m2 ütköző golyó lehet egyenlőtlen. A törvény szerint a mechanikai energia megmaradás

Ott υ1 - első labda sebességét ütközés előtt, a sebességet a második labdát υ2 = 0, u1 és u2 - golyó felgyorsítja az ütközés után. A törvény lendületmegmaradás sebességre előrejelzések a koordináta tengely mentén irányul az első labda sebessége a becsapódás előtt, írásos formában:

Van egy rendszer két egyenlet. Ez a rendszer lehet megoldani, hogy megtalálja az ismeretlen sebességgel u1 és u2 golyó az ütközés után:

Abban a speciális esetben, ha mindkét golyó azonos tömeg (m1 = m2), az első labda (u1 = 0) megállították az ütközés után, és a többi mozog sebességgel u2 = υ1. t. e. kicserélt labdák sebességek (és ezáltal lendületet).

Ha az ütközés a második labdát is volt egy nem nulla sebesség (υ2 ≠ 0), akkor ez a probléma könnyen csökkenthető, hogy az előző egy átmenet egy új referenciakeretet, ami mozog egyenletesen egy egyenes vonal sebességgel Y2 képest a „fix” rendszer. Ebben a rendszerben a második labdát nyugszik az ütközés előtt, és az első törvény a sebesség készítmény sebesség υ1 „= υ1 - υ2. Miután meghatároztuk a fenti képlet alapján sebesség u1 és u2 golyó az ütközés után az új rendszer, meg kell, hogy az átmenet vissza a „helyhez kötött” rendszer.

Így, a jogszabályok mechanikai energia megmaradás és a lendület, a sebesség meghatározható az ütközés után a golyókat, ha tudjuk, hogy az ütközés sebességét.

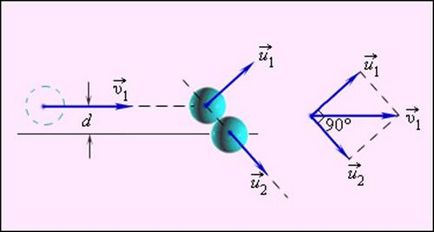
Központi (frontális) hit nagyon ritkán ültetik át a gyakorlatba, különösen abban az esetben, ütközések atomok vagy molekulák. Amikor noncentral rugalmas ütközés sebessége a részecskék (gömbök) előtt és után az ütközés nem irányul ugyanazon vonal mentén.

A konkrét esetben a noncentral rugalmas ütközés esetére sem szolgálhat két biliárdgolyó egyenlő tömegű, melynek egyikéhez az ütközés javításra került és a második sebesség nem célja a középvonala golyók (ábra. 1.21.3).