négyzet trinomiális

Így hívtam polinom. képlet által meghatározott $ a ^> + bx + c $ $ (a \ ne 0) $ szám $ a, b $ és $ c $ - együtthatói másodfokú polinom, ezek gyakran nevezik :. egy - Senior, b - a második, illetve átlagos koefficiensét c - szabad távon. Funkció a y = ax 2 + bx + c nevezzük másodfokú függvényt.

Miután egy lineáris függvény egy másodfokú függvény - egyszerű és fontos elemi függvény. Sok fizikai függőség lehet kifejezni egy másodfokú függvény; például egy követ dobott fel a sebesség v0. Ez található a t időpontban a régióban

a Föld felszínét (itt, g - a nehézségi gyorsulás); a Q hőmennyiség, során felszabaduló áthaladását áram a vezeték R ellenállás, kifejezve áramerősségű I általános képletű Q = RI 2.

Szögletes trinomiális. Ábra. 1.

Szögletes trinomiális. Ábra. 2.

Szögletes trinomiális. Ábra. 3.

Szögletes trinomiális. Ábra. 4.

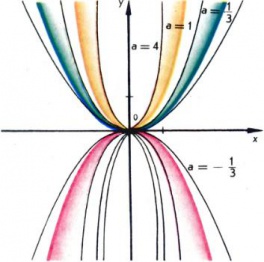
Csak egy speciális esete a másodfokú függvény olyan függvény y = ax 2 résznél. Az 1. ábra grafikonok y = ax 2 különböző értékeit. A grafikon y = ax 2 nevezzük a parabola.

Mindezek a parabola csúcsa van az eredete; egy> 0 a legalacsonyabb pont a grafikon (a legkisebb érték a funkció), míg a <0, наоборот, наивысшая точка (наибольшее значение функции). Ось Oy есть ось симметрии каждой из таких парабол.

Mint látható, a> 0 parabola felfelé egy <0 — вниз.

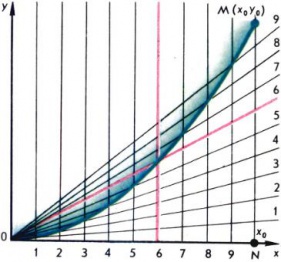
Van egy egyszerű és felhasználóbarát grafikus módon, hogy bármilyen pontok száma a parabola y = ax 2 számítás nélkül, ha tudjuk, hogy a parabola pont eltér a tetején. Legyen az M pont (X0. Y0) fekszik a parabola y = ax 2 (ábra. 2). Ha azt akarjuk, hogy építeni között a pontok között M és O még tovább n pontot, majd ossza a szegmens ON abszcisszán az n + 1 egyenlő részre, és a pontokat elosztjuk a merőleges a Ox tengelyre. Ugyanebben egyenlő részre, és felosztják NM szegmens Division pontok csatlakoztassa gerendák a származási. A kívánt pontnál a parabola fekszik metszéspontjában merőlegesek és gerendák ugyanazokkal a számokkal (ábrán. 2. választóvonal száma 9 pont).

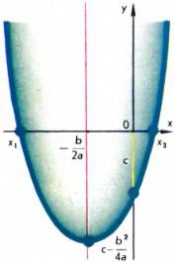
A grafikon y = ax 2 + bx + c eltér a grafikon y = ax 2 csak a helyzetüket, és lehet nyerni egyszerűen, A görbe látható. Ebből következik, képviselet formájában másodfokú polinom

könnyű arra következtetni, hogy a grafikon y = ax 2 + bx + c parabola y = ax 2. tetején átkerült a pontot

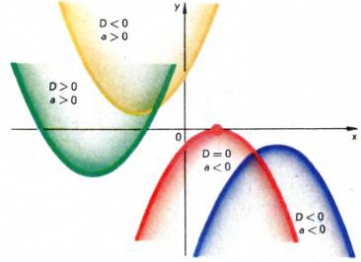
és a szimmetriatengelye párhuzamos marad a tengellyel Oy (ábra. 3). Ebből kifejezés a másodfokú polinom könnyű követni annak minden alapvető tulajdonságait. Az expressziós D = b 2 - 4ac úgynevezett diszkrimináns másodfokú polinom ax 2 + bx + c, és a kapcsolódó diszkriminánsa másodfokú egyenlet ax 2 + bx + c = 0. A diszkrimináns megjelölés attól függ, hogy a grafikon keresztezi az x-tengely másodfokú polinom, vagy annak egyik oldalán belőle. Azaz, ha D <0, то парабола не имеет общих точек с осью Ox, при этом: если a> 0, akkor a parabola fölött fekszik tengelyt Ox, és ha a <0, то ниже этой оси (рис. 4). В случае D> 0 graph másodfokú polinom metszi az x tengely két ponton x1 és x2. amelyek gyökerei a másodfokú egyenlet ax 2 + bx + c = 0, illetve és

Ha a D = 0 Ami a parabola tengelye azon a ponton Ox

A tulajdonságait másodfokú polinom hazugság alapján a megoldás a másodfokú egyenlőtlenségek. Hadd magyarázzuk ezt egy példa. Tegyük fel, hogy szeretné megtalálni az összes megoldást az egyenlőtlenség 3x 2 - 2x - 1 <0. Найдем дискриминант квадратного трехчлена, стоящего в левой части неравенства: D = 16. Так как D> 0, akkor a megfelelő másodfokú egyenlet 3x 2 - 2x - 1 = 0 két különböző gyökereket, ezek határozzák meg a egyenletek a fent megadott:

Ebben a téren trinomiális a = 3> 0, akkor ágak grafikon felfelé és másodfokú polinom negatív értékek csak az intervallumban a gyökerek között. Tehát az összes megoldást kielégítik az alábbi egyenlőtlenségeket

Tér a egyenlőtlenségeket csökkenteni lehet a különböző egyenlőtlenség által azonos szubsztitúciók, amelyek a különböző egyenletek csökken a tér.