Megoszlása folytonos véletlen változó
Véletlen változó nevezzük változó vehet ezen vagy más értékek különféle körülmények.
Véletlen értékek vannak osztva különálló (vagy szakaszos) és folyamatos.
Egy véletlen változó úgynevezett folyamatos. ha vehet bármilyen értéket bármilyen határozott vagy határozatlan időre. Folyamatos véletlenszerű változó lehetetlen meghatározni a lehetséges értékekkel, ezért ezek az értékek azt jelzik, intervallumok, amelyek kapcsolatban vannak bizonyos valószínűséggel.
Példák a folytonos valószínűségi változók lehetnek: átmérője részei fordult egy előre meghatározott méretű, magasság, távolság, stb a lövedék repülési.
véletlenszerű változó funkció (mind a diszkrét és folytonos), vagy egy integrált funkció egy olyan funkció, amely meghatározza a valószínűsége, hogy az érték a véletlen X változó kisebb, vagy egyenlő, mint a határ értékét x.
Sűrűség veroyatnostif folytonos véletlen változó (x) az származéka annak eloszlásfüggvény:
Ismerve a sűrűségfüggvény, lehetséges, hogy annak a valószínűsége, hogy az érték és a folyamatosan változó tartozik a zárt intervallum [a; b]:
valószínűsége, hogy a folytonos X valószínűségi változó vesz bármilyen értéket, az [a; b], egyenlő egy bizonyos szerves annak valószínűségi sűrűsége tól b-ig:
kapott ebből, hogy
A beépített e-egyenlet fejezi ki annak valószínűségét, hogy egy valószínűségi változó vesz bármilyen érték az intervallum. De ez az esemény jelentős, ezért a valószínűsége egyenlő eggyel.
1. példa Folyamatos sűrűsége valószínűsége, hogy a véletlen X változó határozza meg az egyenlet, ahol. A. Keresse együttható a valószínűsége, hogy a folytonos X valószínűségi változó vesz bármilyen érték intervallumban] 0, 5 [folytonos eloszlású véletlen változó X.
Határozat. By hipotézis, megkapjuk az egyenlő
Következésképpen, ha. Így
Most annak a valószínűsége, hogy a folyamatos X valószínűségi változó vesz bármilyen érték intervallumban] 0, 5 [:
Most kap eloszlásfüggvénye véletlen változó:
2. példa annak a valószínűsége sűrűsége folytonos véletlen változó X. hogy megkapja csak nem negatív értékeket, és eloszlásfüggvény.
Határozat. Definíció szerint, megkapjuk a valószínűség-sűrűség
amikor és amennyiben az F (x) ezen értékek x állandó (nulla).
A grafikon a valószínűségi sűrűség folytonos véletlen változó nevezzük eloszlás görbe (ábra. Lent).
Négyzet alakú (szaggatott vonallal van feltüntetve) által határolt görbe, a húzott vonal A és B pontok merőleges az X-tengely és az x-tengely. grafikusan mutatja a valószínűsége, hogy az érték a folyamatos X valószínűségi változó tartományban van ból b.
Ebből megjeleníti a következő tulajdonságokat a sűrűségfüggvény:
- értéke az f (x) pozitív szám, amely kívül létezik a forgalmazási nullával egyenlő;
- ábra területen, amelyek korlátozzák a grafikont a f (x) és az x-tengely. egy egység :.
folytonos valószínűségi változó eloszlás jellemzi az átlagos értékeit és variációk az indexek és más indexét.
A számtani átlaga az összes lehetséges folytonos véletlen változó nevezzük várakozást. vagy a jelölt.
Az elvárás H. folytonos sűrűségű valószínűsége, hogy egy véletlenszerű változó, amely az f (x), megtalálható az érték az integrál
ha konvergál teljesen.
A variancia értéke a szerves
ha konvergál.
A szórása folytonos valószínűségi változó definiáljuk, mint a számtani középérték négyzetgyökének a variancia.
3. példa adjuk folytonos véletlen változó. A valószínűség-sűrűség és a többi érték x. Megtalálja átlag és szórás.
Határozat. Először határozza meg a paramétert. Elosztjuk az intervallum integrációját alkatrészek, megkapjuk
mivel a másik két integrál egyenlő nullával miatt elhanyagolható valószínűséggel sűrűség ezeket a tartományokat. ezért
Ha megtaláljuk a szükséges matematikai elvárás egy véletlenszerű változó:
(Integration határértékek 0 és 10 vannak szerelve ugyanazon okokból, mint amikor a paraméter). Kiszámoljuk a variancia egy = 5 és f (x) = 0,1:
folytonos véletlen változó egyenletes eloszlású az elosztási ahol az érték a véletlen változó két oldalról, és korlátos intervallumban határok ugyanolyan valószínűséggel. Ez azt jelenti, hogy ebben a tartományban, a valószínűség-sűrűség állandó.
Így egy egyenletes eloszlását a valószínűsége sűrűsége adják
A eloszlásfüggvény folyamatos valószínűségi változó egyenletes eloszlás a forma
Tartalmaz egy egyenletes eloszlás:
- átlagos (elvárás);
- diszperzió;
- szórás;
- veroyanost, hogy az érték lesz a folytonos valószínűségi változó egy előre meghatározott tartományban, ahol.
4. példa Megfigyelések azt mutatta, hogy a súlya a doboz szállítására használt zöldségek, egy egyenletesen eloszló véletlenszerű változó tartományban 985-1025 g Véletlenszerűen kiválasztott egy fiók. Keresse jellemzők egyenletesen oszlik sluchanoy mennyiségben körülmények között, amelyek meg kell határozni a döntést.
Határozat. Mi annak a valószínűsége, hogy a súlya a doboz lesz a tartomány 995-1005
Találunk átlagos értéke folyamatosan változó:
Mi található a szórás:
Határozza meg, mi tömegszázaléka dobozok található, a parttól egy szórás az átlagtól értéket (azaz a tartományban ..):
Normál eloszlása folytonos valószínűségi változó egy eloszlási sűrűsége függvény, amely:
ahol x - érték változó érték - átlag - szórás, e = 2,71828. - természetes logaritmus alapja = 3,1416.
Az alábbi ábra mutatja a sűrűségfüggvénye normális eloszlás gráfot kapunk adatokat mintát számításokat a szoftvercsomag STATISTICA. Ez a hisztogram oszlopai értékeket képviselik a minta, a forgalmazás, amely közel (vagy, ahogy mi mondjuk, a statisztikák különböznek jelentéktelen re) a tényleges grafikus normális eloszlás sűrűségfüggvénye amely a görbe egy piros színű.
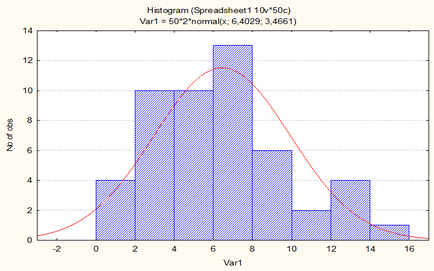
Hogy növelje a kép akkor kattintson a bal egérgombbal.
sűrűségfüggvénye normális eloszlás
- összes érték az érvelés sűrűségfüggvény pozitív;
- ha az érv tart végtelenbe, akkor a sűrűség függvény Streit nullára;
- sűrűség függvény szimmetrikus az átlagos értékeket;
- a legnagyobb értéket a sűrűségfüggvény - az átlagértékek;
- sűrűségfüggvény görbe konvex és a konkáv tartományban, a többi rész;
- mód, a medián normális eloszlás megegyezik az átlagos értéket;
- normál eloszlás szimmetrikus, így aszimmetria együttható a = 0.
Változások mozgóátlag görbéje normális eloszlás sűrűségfüggvényének a tengely irányában Ox. Ha növekszik, a görbe jobbra mozog, ha csökken, a bal oldalon.
Ha megváltoztatja a szórás, a változó magassága a tetején a görbe. Növelésével a szórása a csúcs fölött helyezkedik el a görbe, a csökkenés - kisebb.
A kumulatív normális eloszlás:
Szabványosított vagy normalizált úgynevezett normális eloszlás, akiknek az átlagos érték és szórás.
Sűrűségfüggvénye a standardizált normális eloszlás:
A kumulatív standardizált normál eloszlás:
Az alábbi ábra a szabványosított kumulatív normális eloszlás, ami egy grafikon számítások kapott mintavételezés a szoftvercsomag STATISTICA. Tulajdonképpen görbe grafikon vörös színű, és a minta értékek közel hozzá.
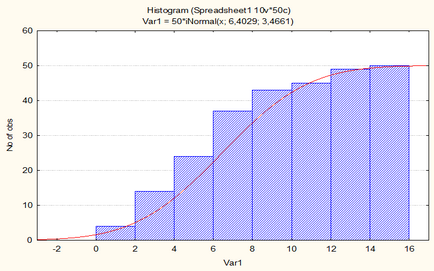
Hogy növelje a kép akkor kattintson a bal egérgombbal.
Szabványügyi véletlen értéket jelenti átmenet a felhasznált eredeti egységeket a munkát szabványosított. Szabványügyi végezzük a következő képlet alkalmazásával
A gyakorlatban, az összes lehetséges értékek egy véletlenszerű változó gyakran nem ismert, és ezért a értékeit átlag és szórás nem lehet pontosan meghatározni. Ezek helyébe a megfigyelések átlaga és szórása s. A z mennyiség kifejezi az eltérés a valószínűségi változó értékek átlagából szórása a mérést.
Gyakorlatilag bármely tankönyv statisztikák a függelékek végén a könyv megtalálható egy táblázatot sűrűség értékeinek függvényében a standardizált normális eloszlás és az integrált funkciókat. Ahhoz, hogy használni ezeket az értékeket, meg kell kiszámítani a standardizált érték változó nagyságú. függvény
hogy meghatározzuk annak valószínűségét, hogy egy standardizált Z értéke nem kisebb, mint -z, és nem több, mint + z. ahol z - önkényesen kiválasztott értéket szabványosított véletlen változó.
5. példa Enterprise termel alkatrész, amelynek szolgáltatás normális eloszlású átlagos 1000 és a standard deviáció 200 óra.
Egy véletlenszerűen kiválasztott részeit kiszámítja a valószínűsége, hogy annak élettartama lesz, nem kevesebb, mint 900 óra. Ez a számítás valószínűség segítségével az asztal, a véletlen változó először egységesíteni. Akkor majd a megfelelő értéket a beépített függvény táblákat. kapjuk:
Tehát annak a valószínűsége, hogy az élet a terméket nem lehet kevesebb, mint 900 óra, 69%.