másodfokú trinomiális

másodfokú polinom

Az úgynevezett polinom által meghatározott igények. Számok és - másodfokú polinom-együtthatók, ezek gyakran nevezik: - Senior, - a második vagy középső együttható - konstans. Függvénnyel úgynevezett másodfokú függvényt.

Miután egy lineáris függvény egy másodfokú függvény - egyszerű és fontos elemi függvény. Sok fizikai függőség lehet kifejezni egy másodfokú függvény; például egy követ dobott fel, amelynek mértéke tárolt idején a régióban

A Föld felszínét (itt - a nehézségi gyorsulás); hőmennyiség keletkezik, amikor áram folyik a vezetékben ellenállást, kifejezett áramerősség állítások.

Csak egy speciális esete a másodfokú függvény olyan függvény. Ábra. Az 1. ábra grafikonok a funkciók különböző értékeket. Függvény grafikonját az úgynevezett parabola.

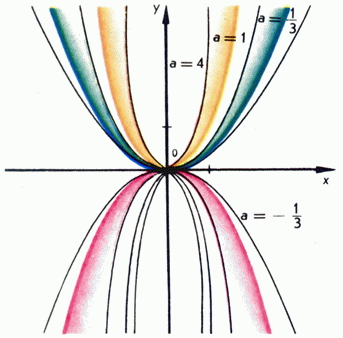
Mindezek a parabola csúcsa van az eredete; A legalacsonyabb ezen a ponton a grafikonon (a legkisebb érték a függvény), míg ezzel ellentétben, a legmagasabb pontja (a legnagyobb érték a funkció). Tengely a szimmetria tengelye minden egyes ilyen parabola.

Mint látható, amikor a parabola felfelé irányul, - lefelé.

Van egy egyszerű és felhasználóbarát grafikus módon, hogy bármilyen pontok száma a parabola számítás nélkül, ha tudjuk, hogy a parabola pont eltér a tetején. Tegyük fel, hogy az a pont fekszik a parabola (ábra. 2). Ha azt akarjuk, hogy létrejöjjön a pontok között, és egy pontot, majd ossza a hossza a vízszintes tengely egyenlő részre, és a pontokat elosztjuk a tengelyére merőleges. Ugyanebben piaci részesedést egyenlő részre, és a pontok osztály egyesíti gerendák eredetét. A kívánt pontnál a parabola fekszik metszéspontjában merőlegesek és gerendák ugyanazokkal a számokkal (ábrán. 2. választóvonal száma 9 pont).

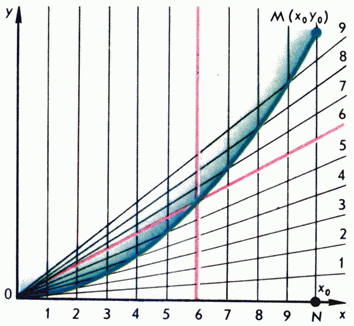
Függvény grafikonját eltér a menetrend csak a helyzetüket, és érhető el egyszerűen azáltal, hogy a görbe az ábrán. Ebből következik, képviselet formájában másodfokú polinom

könnyű arra következtetni, hogy a grafikon egy parabola, amelynek a teteje átkerült a pont

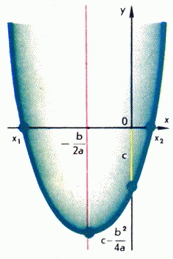
és a szimmetriatengelye párhuzamos marad a tengelyen (3.). Ebből kifejezés a másodfokú polinom könnyű követni annak minden alapvető tulajdonságait. A kifejezés az úgynevezett diszkriminánsa másodfokú polinom, és a kapcsolódó diszkriminánsa másodfokú egyenlet. Tól diszkrimináló jel attól függ, hogy a grafikon keresztezi az x tengely másodfokú polinom vagy annak egyik oldalát. Nevezetesen, ha a parabola nincs közös vonást mutat a tengely, ahol: ha a parabola fölött fekszik tengelyen, és ha ez alatt e tengely (4. ábra). Abban az esetben, másodfokú polinom gráf metszi az x tengely két ponton, és amelyek gyökerei a másodfokú egyenlet és rendre

Ami a parabola tengelye azon a ponton.

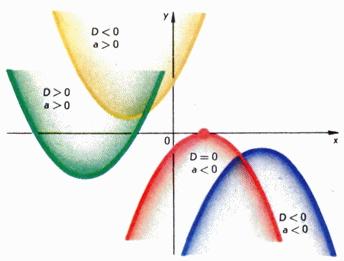
A tulajdonságait másodfokú polinom hazugság alapján a megoldás a másodfokú egyenlőtlenségek. Hadd magyarázzuk ezt egy példa. Tegyük fel, hogy szeretné megtalálni az összes megoldást az egyenlőtlenség. Megtaláljuk a diszkriminánsa másodfokú polinom, a bal oldali az egyenlőtlenség :. Azóta a megfelelő másodfokú egyenlet két különböző gyökereket, ezek határozzák meg a megadott képletek korábban:

Ebben a három tagú négyzet, akkor annak ága felfelé és grafika másodfokú polinom negatív értékek csak az intervallumban a gyökerek között. Tehát az összes megoldást kielégítik az alábbi egyenlőtlenségeket

Tér a egyenlőtlenségeket csökkenteni lehet a különböző egyenlőtlenség által azonos szubsztitúciók, amelyek a különböző egyenletek csökken a tér.