lendület a test, ez a fizika
Legyen m a testtömeget egy rövid időköz At erő hatása alatt ez az erő a test sebessége változik Következésképpen idején At test mozgó gyorsulás
A alaptörvénye dinamika (Newton második törvénye) kell lennie:
Egy fizikai mennyiség, egyenlő a súlyt a mozgásának sebességét a test nevezzük impulzus (vagy a mozgást). lendület a test - vektor mennyiség. A mértékegység a SI impulzus kilogramm méter másodpercenként (kg · m / s).
Fizikai mennyiség egyenlő az erő idején működését, az úgynevezett impulzus teljesítmény. impulzus is egy vektor mennyiségben.
Az új feltételek Newton második törvénye alapján megállapítható, az alábbiak szerint:
Változások a test lendület (a mozgás mennyisége) az impulzus erő.
A kijelölő szerv lendület írni Newton második törvénye felírható
Ez ebben az általános formában megfogalmazott második törvénye Newton maga. Az erőssége ez a kifejezés az eredő az összes erők a testre. Ez a vektor az egyenlet felírható a nyúlványok a koordinátatengelyeken:
Így, a változó a nyúlvány test pulzust bármely három kölcsönösen merőleges tengely mentén megegyezik a vetítési impulzus ugyanazon a tengelyen. Tekintsük példaként a egydimenziós mozgást, azaz. E. A test mozgása az egyik koordinátatengelyek (például, OY tengely). Hagyja, hogy a test szabadon esik kezdeti sebességgel υ0 a gravitáció; esnek ideje egyenlő t. Irányítsa a OY tengely függőlegesen lefelé. Impulzus gravitációs FT = mg t idő egyenlő MGT. Ez az impulzus a mozgásmennyiség-változás a test
Ez az eredmény egybevág azzal az egyszerű sebességgel kinematicheskoyformuloydlya egyenletesen gyorsuló mozgás. Ebben a példában az erő változatlan abszolút értékben a teljes időintervallum t. Ha az erő változik a nagysága, akkor a kifejezés a lendület erő szükséges, hogy helyettesítse az átlagérték favg erőt adott időintervallumban a keresete. Ábra. 1.16.1 ábra meghatározásának módja az impulzus erő az idő függvényében.
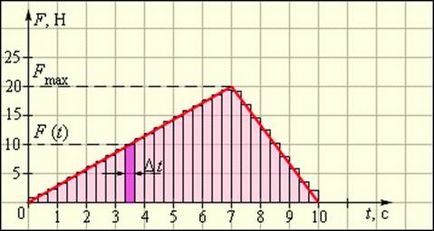
Kiszámítása az erő impulzus egy telek F (t)
Válassza ki az időt tengely kis intervallum dt. amelynek során egy F erő (t) lényegében változatlan maradt. Impulzus F erő (t) At az idő At megegyezik a terület a kikelt oszlop. Ha az egész időtengely intervallumban 0 t osztva kis időközönként δti. majd összegezni az impulzusokat az erő egyáltalán időközönként δti. a teljes lendület erő egyenlő lenne a területet képező lépcsős görbével az időtengelyen. A határérték (δti → 0), ez a terület által határolt területen a grafikon F (t), és a t tengely. Ez a módszer a meghatározó impulzus erők menetrend F (t) általános és alkalmazható minden törvényi erővel idővel változik. Matematikailag, a probléma csökkenti az integrációs funkció F (t) a [0; t].
Impulse erők, amelynek grafikonja ábrán látható. 1.16.1, az intervallum t1 = 0, t2 = c 10 c:
Ebben az egyszerű példában
Egyes esetekben az átlagos erő favg meghatározható, ha ismerjük az időt az akció, és jelenteni a test egy lökést. Például, a visszafordulási futball-labda súlyú 0,415 kg tájékoztathatja vele υ = sebessége 30 m / s. Shot ideje nagyjából megegyezik a 8 × 10 -3 másodperc.
A lendület p. eredményeként megszerzett üti a labdát:
Következésképpen az átlagos erő favg. amellyel a játékos működtetett lábát a labda ütközés során vannak:
Ez egy nagyon nagy erő. Ez körülbelül egyenlő a tömege testtömeg 160 kg.
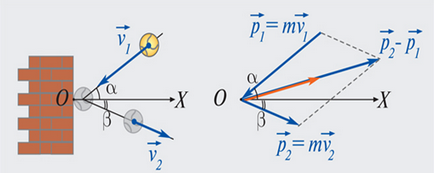
Ha a mozgás a test a tevékenység során az erő történt ívelt pálya, a kezdő és befejező test impulzusok különböznek nem csak a nagysága, hanem iránya. Ebben az esetben a változások meghatározásához az impulzus diagram impulzusok amelyet használunk. amelyek ábrázolt és a vektor, és olyan vektorral alatt a szabály a paralelogramma. Példaként, ábrán. 1.16.2 egy diagram impulzusok a labdát újjáéledő az egyenetlen fal. A labda ütött tömegének m sebességgel fal szögben α a normál (OX-tengely), és visszaállt belőle sebességgel szögben β. Során a fallal érintkezésben a labdát egy bizonyos ható erő irányában, amely egybeesik az irányt a vektor