Keresse az egyenlet a háromszög oldalai seekland info közösségi kölcsönös hallgatók és diákok

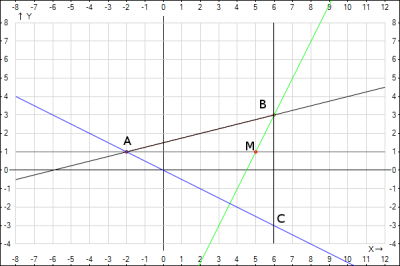
1. Az egyenes egyenlete AB
Két csúcsai, azaz az egyik oldalon az egyenlet lehet beszerezni, mint egy egyenlet egy átmenő egyenes a két adott pont # 92 $$; frac = # 92; frac $$ helyettesíti a csúcs koordinátáit (-2.1) V (6; 3) az egyenlet és szerezzen $$ # 92; frac = # 92; frac => y = # 92; fracx + # 92; frac $$

Ahhoz, hogy megtalálja az egyenlet a többi oldala,
Találunk az egyenlet magassága:
2. Az áthaladó vertex és merőleges BC, nevezzük AM. Két pont már ismert, vonatkozik lineáris egyenlet áthaladó két adott pont A (-2,1), M (5, 1) # 92 $$; frac = # 92; frac $$ Tk. y a nevezőben van 0, akkor a közvetlen, a tengellyel párhuzamos Ox és egyenlet # 92; (y = 1 # 92;)
3. B áthaladó vertex és merőleges AC, ez az úgynevezett BM. Két pont már ismert, vonatkozik lineáris egyenlet áthaladó két adott pont B (6; 3), M (5, 1) # 92 $$; frac = # 92; frac => y = 2x-9 $$

Az egyenletek ilyen magasságokba, mi csak keres egy dolog: mint tudjuk lejtőin merőleges vonalak kötik össze az alábbi összefüggés # 92; (k_1 = - # 92; frac # 92;), azaz egyenletek A fennmaradó két oldalán, már az egyik legnépszerűbb és lejtőin. Kapjuk ezeket az egyenleteket:
4. Az egyenes egyenlete AC. Mert ez az egyenlet van a koordinátákat a csúcsának (-2,1), és megtalálni a lejtőn, ismerve a lejtőn az egyenes merőleges BM, ami egyenlő # 92; (k_ = 2 # 92) => # 92; (k_ = - # 92; frac> = - # 92; frac # 92;). Ezután az egyenlet a sor AC egyenlő $$ y-1 = - # 92; frac (x + 2) => y = - # 92; fracx $$
5. Az egyenlet BC egyenest. Ismeretes, hogy a magassága AM merőleges erre az oldalra, a tengellyel párhuzamos Ox, akkor ezen az oldalon párhuzamos a tengellyel Oy, és ebben az esetben át a B csúcs (6; 3), azaz a annak egyenlet # 92; (x = 6, # 92;)

Az egyenletek három egyenes oldalán a háromszög található. felállni háromszög