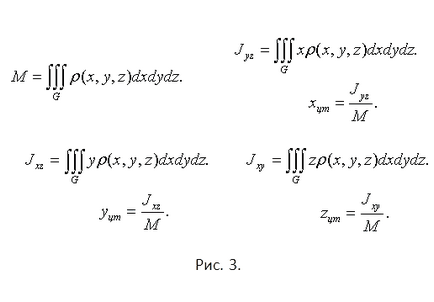Hogyan lehet megtalálni a test tömegközéppontja

Megjegyezzük, hogy a súlypont függ, milyen módon elosztva a térfogata a testtömeg. A tömegközéppont sem lehet a szervezetben, egy példa egy ilyen tárgy szolgálhat egy egyenletes gyűrűs, amelyben a tömegközéppont található geometriai központja. Ez - a vákuum. Kiszámításakor a tömegközéppontja is tekinthető matematikai pont, ahol az egész test tömege.

A fogalmak a tömegközéppont és súlypont nagyon közel van, így a számítások, a legtöbb esetben, akkor lehet tekinteni szinonimája. Az egyetlen különbség az, hogy a koncepciót a súlypont van szükség a gravitáció és a súlypont hiányában jelen a gravitáció. Body szabadon esik, és forgatás nélkül, mozog az intézkedés alapján a gravitációs erő valamennyi pont, a tömegközéppontja egybeesik a súlypont. Annak meghatározására, a tömegközéppontja a klasszikus mechanika használja az alábbi képletben.

Itt R.ts.m. - a sugár vektor a tömegközéppont, MI - tömege i-egy pont, RI - sugara vektor i-pontrendszer. A gyakorlatban sok esetben könnyű megtalálni a tömegközéppontja, ha a tárgy valamilyen szigorú geometriai forma. Például, homogén rudat éppen a közepén. A paralelogramma - metszéspontjában átlóinak a háromszög a metszéspont a medián és a szabályos sokszög súlypontja központjában forgásszimmetrikus.

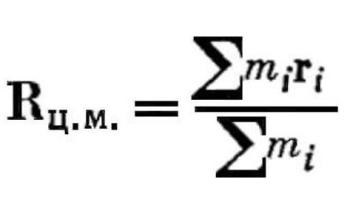
A bonyolultabb feladat számítási test bonyolultabbá válik ebben az esetben meg kell osztani homogén test térfogata. Minden közülük kiszámítása külön-külön a tömegközéppontjai, majd a kapott értékeket behelyettesítjük a megfelelő képletek és tárolt végső értéket.

A gyakorlatban a szükséges meghatározni a tömegközéppont (súlypontja) általában együtt jár a tervezési munkát. Például, a tervezés során a hajó fontos biztosítja annak stabilitását. Ha a súlypont nagyon magas lesz, a hajó felborul. Hogyan számoljuk ki a kívánt beállítást egy ilyen bonyolult tárgyat, mint egy hajó? Erre a célra a súlypontok az egyes elemek és aggregátumok, majd a kapott értékeket adunk tekintetében a helyét. Tervezésekor a súlypont általában megpróbálja elhelyezni a lehető legalacsonyabb, így a legnehezebb szerelvények vannak elrendezve az alján.

A tömegközéppont - a legfontosabb geometriai és műszaki jellemzőit a test. Kiszámítása nélkül koordinátáit lehetetlen tervezni a gépgyártás, a feladatokat az építési és az építészet. Pontos meghatározása a tömegközéppont koordinátát végre az integrálszámítás.

Mindig indul az egyszerű, fokozatosan halad a bonyolultabb helyzetekben. Tegyük fel, hogy a folyamatos meghatározását alany középsíkhoz ábra D tömegsűrűsége ρ, amely konstans és egyenletesen elosztott belül. Érv x változik a B, Y a c a d. Szünet függőleges rács szám (x = x (i-1), X = xi (i = 1,2, ..., n)) és a vízszintes vonalak (y = y (j-1), y = xj (j = 1, 2, ..., m)) elemi téglalapok bázisokkal Δhi = xi-x (i-1) és a magasságok Δyj = yj-y (j-1) (lásd. ábra. 1). Ebben a középső szegmenst elemi Δhi kap mind ξi = (1/2) [xi + x (i-1)] és a magassága, mint Δyj ηj = (1/2) [yj + y (j-1)]. Mivel a sűrűség egyenletesen oszlik, akkor a tömegközéppontja elemi téglalap egybeesik a geometriai középpontjával. Ez Htsi = ξi, Ytsi = ηj.

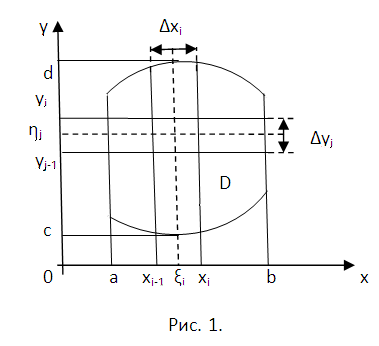
M tömeg síkidom (ha ismert), kiszámítja a termék sűrűségének a terület. Cserélje ki az elemi terület és ds = ΔhiΔyj = dxdy. Bevezetése Δmij mint a DM = ρdS = ρdxdy és kap a súlyát a megadott képlettel az ábrán. 2a. A kis lépésekben úgy, hogy Δmij masszát koncentrálódik az anyagi pont koordinátájú Htsi = ξi, Ytsi = ηj. A mechanika ismert, hogy egyes koordináták a tömegközéppontja a rendszer egy frakciót, amelynek számlálója az összegét tartalmazza a statikus pillanatok a tömegek mν egy megfelelő tengely, és a nevező az összege ezeknek a tömegeknek. Statikus tömeg pillanatban mν, viszonylag 0x tengely uν * mν, de viszonylag 0y hv * mν.

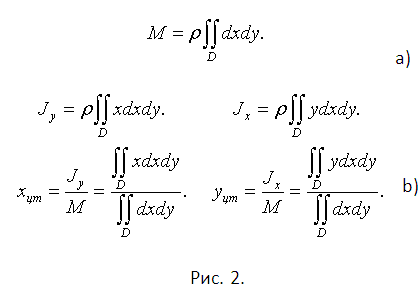
E szabály alkalmazása erre a helyzetre, és kap a közelítő értékek a statikus pillanatok és Јh Јu mint Јu≈, Јh≈ (összegzés át ν 1 N). Tartalmazza az utóbbi szerves expressziós mennyiségét. Navigáljon a határait a Δhν Δyν → → 0 0, és rögzíti a végső képletben (lásd. Ábra. 2b). Koordinátái a tömegközéppontja található elosztjuk a megfelelő statisztikai pillanatban a teljes súlya ábra M.

Módszertan megszerzésének térbeli koordinátáinak a tömegközéppontja G ábra csak abban különbözik, hogy a integrálok rendelkező terner és tekinthető statikus pillanatok képest a koordináta síkok. Nem szabad elfelejteni, hogy a sűrűség nem szükségképpen állandó, azaz a ρ (x, y, z) ≠ const. Ezért a végső és a Samy általános válasz formájában (lásd. Ábra. 3.).