Hogyan lehet megtalálni a nagyságát a vektor

előző ◈ a következő

Vektor - egy geometriai objektumot, amely egyaránt jellemzi a nagysága és iránya. [1] Az nagysága vektor a hossza, és irányának felel meg, amelyre az mutat. Nagysága a vektor kiszámítása nagyon könnyen, mert, hogy néhány egyszerű lépésben. Más fontos műveleteket vektorok közé tartozik a összeadás és kivonás a vektorok, a megállapítás közötti szög a két vektor és a számítás a vektor termék.

lépések szerkesztése

1. módszer a 2:
Kiszámítása a vektor érkező eredetű szerkesztése

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

Határozza meg a vektor komponensek. Bármely olyan vektor, a gépen lehet numerikusan képviseli egy kétdimenziós koordináta-rendszerbe a két szám: a vízszintes (X tengely) és a függőleges komponens (Y-tengely). [2] A vektor felírható egy pár számok: v = .
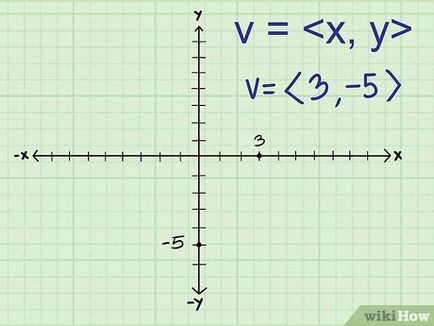
  • Például, ha a vízszintes a vektor komponense egyenlő 3, és a függőlegeshez képest -5, ez a vektor van írva, mint <3, -5>.

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

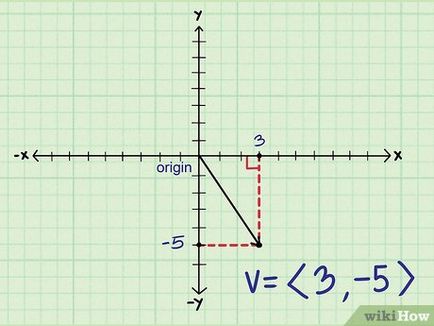
Rajzolj egy vektor háromszög. Ha fel a vízszintes és függőleges elemek, akkor van egy derékszögű háromszög. Nagysága a vektor hossza a háromszög átfogója, és annak számítási, akkor használja a Pitagorasz-tétel.

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

Kiszámításához vektorok, jegyezze fel a Pitagorasz-tétel. Pitagorasz tétel kimondja, hogy a négyzetének összege a lábak a derékszögű háromszög egyenlő a négyzet a átfogója: A 2 + B 2 = C 2. Ebben az esetben, az „A” és „B” - a vízszintes és függőleges vektor komponenseket, és a „C” jelenti a átfogója. Mivel az átfogója csak egy vektor, meg kell találni a „C”.
  • x 2 + y 2 = v 2
  • v = √ (x 2 + y 2))

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

Keresse meg a vektor nagyságát. Erre a helyettesítő egy egyenletet a numerikus értékek a fent kapott, azaz a megfelelő vektor komponensek.
  • Ebben a példában a v = √ ((március 2 + (- 5) 2))
  • v = √ (25 + 9) = √34 = 5831
  • Ne tévesszen meg, ha az eredmény nem egész szám. A hossza a vektor lehet egy frakcionális érték.

2. módszer 2:
Megtaláljuk az érték a vektor, amelynek kezdetén nem esik egybe a származási szerkesztése

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

Határozza koordinátáit elején és végén a vektor. Bármely olyan vektor, a gépen lehet numerikusan képviseli egy kétdimenziós koordináta-rendszerbe a két szám: a vízszintes (X tengely) és a függőleges komponens (Y-tengely). [3] A vektor felírható egy pár számok: v = . Ha az elején a vektor nem esik egybe a kezdete egy derékszögű koordináta-rendszer, akkor meg kell határozni a koordinátákat a kezdő- és végpontját vektor.
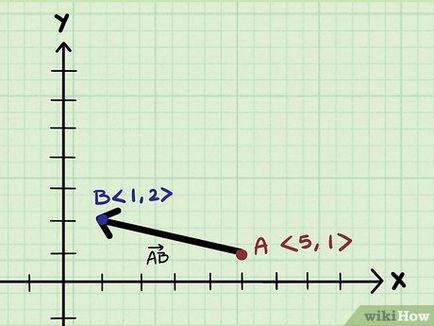
  • Hagyja, hogy a vektor AB összekötő A és B pontok
  • A pont helye egy vízszintes koordináta és függőleges koordinátája 5 1, így a koordinátákat fejezhető számpárok <5, 1>.
  • B pont vízszintes koordináta és függőleges koordináta 1 2, ezért a koordinátái fejezhető számpárok <1, 2>.

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

Ahhoz, hogy megtalálja a nagysága a vektor egy módosított képlet. Mivel ebben az esetben mivel a koordinátáit két pont kell vonni koordinátái x és y egy pont a megfelelő koordinátáit a második pont: v = √ ((x2 -X1) 2 + (y2 -Y1) 2). [4]
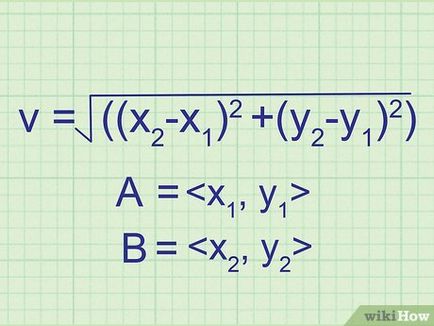
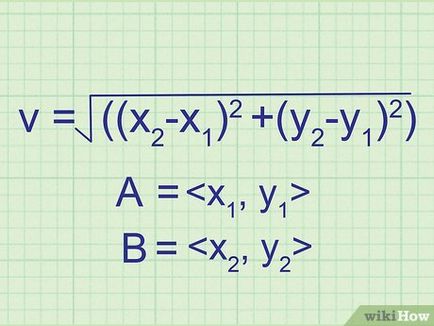
  • Hagyja, hogy a pont koordinátái , és a B pont - koordinátákat

Hogyan lehet megtalálni a nagyságát a vektor

Hogyan lehet megtalálni a nagyságát a vektor

Keresse meg a vektor nagyságát. Tedd a pontok koordinátáinak az egyenletben, és kiszámítja a vektor hossza. Ebben a példában, számítás a következő:
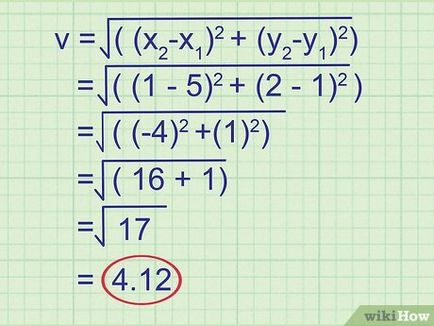
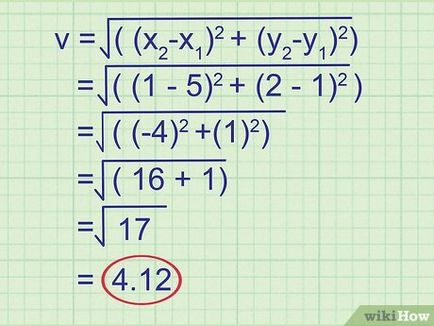
  • v = √ ((x2 -X1) 2 + (y2 -Y1) 2)
  • v = √ ((1-5) 2 + (2-1) 2)
  • v = √ ((- 4) 2 + (1) 2)
  • v = √ (16 + 1) = √ (17) = 4,12
  • Ne tévesszen meg, ha az eredmény nem egész szám. A hossza a vektor lehet egy frakcionális érték.
előző ◈ a következő