Graph differenciálhányados
Targets, amelyben a ábrán egy grafikon a függvény deriváltját y = f „(x), és szükség van, hogy meghatározzuk a szélsőértékek pontok és időközönként monotonitási függvény az y = f (x), nagyon egyszerűen megoldható.
Elég annyit megjegyezni, hogy
1) A funkció y = f (x) növeli a intervallumokban, ahol a származék y = f „(x)> 0;
2) A függvény az y = f (x) csökken időközönként, ahol a származék a y = f „(x)<0;
3) az y = f (x) egy kritikus pontot, ahol a származékot f „(x) = 0, vagy nem létezik (de ez igaz csak a domain a belső pontokat, vagyis pont végein a domain nem tekinthető);
4) az y = f (x) egy szélsőérték pontokat, ahol a származék y = f „(x) előjelváltása.
Különösen, az y = f (x) van egy maximális pont, ahol a származék előjelváltása a plusz mínusz;
függvény y = f (x) van egy minimális pontot, ahol a deriváltja elõjelet mínusz plusz.
Az ábrán egy grafikon, differenciálhányados. Segítségével a grafikon, hogy megtalálják a monotónia időközönként funkció, a kritikus pont, a kritikus pont, és a végletekig.
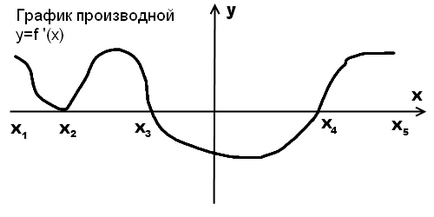
1. ábra. Az ütemterv szerint a származék, hogy vizsgálja meg a funkciót.
A függvény y = f (x) növeli a időközönként (x1, X3) és (X4, X 5) (azaz ott, ahol a származék y = f „(x) pozitív, és így a grafikon fölött fekszik tengely Ox). x2 pont nem zárja ki a nagyobb rés - a származék ezen a ponton nullával egyenlő, de nem változtatja meg a jel.
A függvény y = f (x) csökkenti a rést (x3; x4) (azaz ott, ahol a származék y = f „(x) negatív, ami azt jelenti, hogy a gráf alatt található a tengely Ox).
Kritikus pont: x2, x3, x4. Ezeken a pontokon a derivált nulla (származéka egy grafikon, illetve metszi a tengelyt ox).
X = x3 - maximum pontját az y = f (x), mivel a származék y = f „(x) ezen a ponton előjelváltása a plusz mínusz (ox-származék gráf metszi a felülről lefelé).
X = x4 - minimális pontját az y = f (x), mivel a származék y = f „(x) ezen a ponton előjelváltása a plusz mínusz (ox-származék grafikon metszi lentről felfelé).
Extremum pontot: X3 és X4. Ezek nemcsak magukból eltűnik, hanem megváltoztatja a jel. X = x2 - kritikus, de extremális pont nem, mert nincs változás jele a származék. Azaz, a grafikon a származtatott szélsőérték pont - azokat a pontokat, ahol a grafikon nem vonatkozik, és áthalad a tengely ökör.
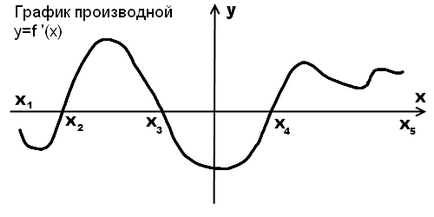
2. ábra. Az ütemterv szerint a származék, hogy vizsgálja meg a funkciót