geometriai formák
Magasság (KR) - egy szegmens, amely összeköti a síkra, amelyben fekszenek a prizma bázis. azt
merőleges ezekre síkok.
Átlós (BP) - egy szegmens, amely összeköti a csúcsai a 2 prizma, amelyek nem tartoznak ugyanahhoz a
Az átlós síkban - egy sík, amely áthalad az oldalsó szélén a prizma, és a
Az átlós szakasz (EBLP) - kereszteződés prizma átlós síkban. A szakasz kapott
A merőleges (ortogonális) rész - a metszéspontja a prizma és a sík merőleges
oldalsó éle a prizma.
- prizma bázis - egyenlő sokszög.
- Az oldalsó felületei a prizma formájában paralelogramma.
- Az oldalsó prizma élei egyenlő és párhuzamos.
- A teljes felülete a prizma = négyzetösszege az oldalfelületén, és egy dupla
ahol P - kerülete a merőleges szakasz, l - hossza az oldalsó szélek.
- A terület a palástfelület egy egyenes hasáb:
ahol P - kerülete a prizma bázis, h - a magassága a prizma.
- Merőleges keresztmetszet merőleges összes mellékhatást A prizma élei.
- A szögek a merőleges keresztmetszet - lineáris szögek a diéderes szögek a megfelelő
- Merőleges keresztmetszet merőleges az oldalfelületeket.
- A kötet a termék a tér prizma a prizma bázis a magasság.
Fender négyszögletes piramis.
Tulajdonságok rendszeres négyszögletes hasáb.
- Bázisok rendszeres négyszögletes prizma - 2 azonos négyzet alakú;
- A felső és az alsó bázisok párhuzamosak;
- Az oldalsó arcok formájában téglalapok;
- Minden oldalfelületek egyenlő;
- A oldalfelületein merőlegesek az alapra;
- Az oldalsó szélek párhuzamosak és egyenlő;
- Merőleges keresztmetszete merőleges a valamennyi oldalirányú szélek és az alappal párhuzamosan;
- A szögek, a függőleges szakasz - közvetlen;
- Átlós rendszeres négyszögletes prizma szakasz egy téglalapot;
- A merőleges (ortogonális szakasz) párhuzamos a bázisok.
Képletek rendszeres négyszögletes hasáb.
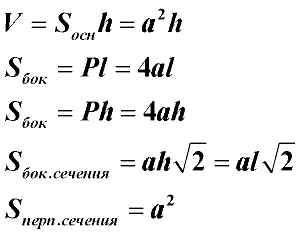
Prism. amelyben a bázis egy paralelogramma, egy paralelepipedon.
Prism - egy prizma, a merőleges oldalsó széleinek a alapsíkkal.
A fennmaradó prizma ferde.
Megfelelő prizma - prizma, az alapja az ő egy szabályos sokszög. oldalsó
egy prizma metszettel - azonos téglalapok.
Megfelelő prizma, amelynek oldalsó felületei - négyzetek (magassága egyenlő a bázist oldalon) nevezik