Feliratos a piramis labda
Ha a feladat adott egy labdát írt a piramis, a megoldás az alábbi elméleti információkat.
Ha a piramis feltüntetik egy gömb, akkor minden csúcsai a a gömb felszínén (a gömb), illetve távolságok a gömb közepén a csúcsok egyenlő a sugara a labdát.
Minden arc írt gömb a piramis van írva egy kört sokszög. A bázisok a merőlegesek csökkent a központtól a gömb sík felületeivel a központja a körülírt körök. Így, a központ a körülírt gömb a piramis - a metszéspont merőleges az arcok a piramis, átszívott központja a körök körül az arcok.
A legtöbb központban leírt körül a labdát a piramis tekintik a metszéspont a merőleges felhívjuk a bázis közepén keresztül mintegy alapkör és a merőleges oldalsó szélén (függőleges felezővonal egy síkban halad át ezen a keresztirányú él, és egy első merőleges (tartott a bázis.) Ha nem lehet leírni egy kört az alapja a piramis, piramis nem helyezhető be egy gömböt. ez azt jelenti, hogy körülbelül egy háromszög alakú piramis mindig lehet leírni a labdát, mint írva a páratlan labda rehugolnaya piramis a bázis egy téglalap vagy négyzet alakú.
Körülbelül a gömb közepén leírt piramisok belsejében helyezkedhet a piramis, a piramis a felületen (a oldallapon, a földön), és piramis. Ha a probléma az állítás nem pontosan megmondani, ahol a központ által leírt világ, kívánatos, hogy fontolja meg, mivel ezek befolyásolhatják a döntést a különböző lehetőségek a helyét.
Körülbelül minden jogot a piramis lehet leírni, mint egy labdát. A központ - a metszéspont a vonal tartalmazó a magassága a piramis és a merőleges oldalsó szélét.
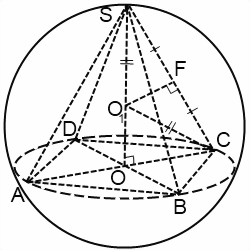
A problémák megoldására a labdát feltüntetik egy piramis gyakran tekintik néhány a háromszögek.
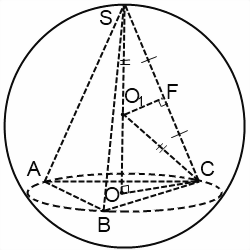
Kezdjük SO1C háromszög. Ez egyenlő szárú, mivel két oldal egyenlő a sugara a gömb: SO1 = O1S = R. Következésképpen O1F - a magassága, a medián és a felezővonal.
Derékszögű háromszögek SOC és SFO1 mint az éles sarka S. Ennélfogva
SO = H - magassága a piramis, SC = b - hossza az oldalsó széleit, SF = b / 2, SO1 = R, OC = r - sugara köré írt kör az alapja a piramis.
A derékszögű háromszög átfogója OO1C g O1C = R, a lábak OC = r, OO1 = H-R. A tétel Pitagorasz:
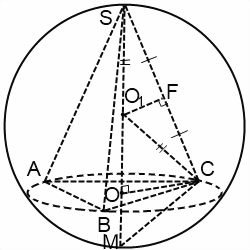
Ha továbbra is magas SO, megkapjuk SM átmérőjű. SCM Triangle - téglalap (mivel SCM kerületi szög alapján az átmérő). Ott OC - magassága hívni a átfogója, SO és OM - vetülete a lábak az SC és CM a átfogója. Az ingatlan a derékszögű háromszög,
és még egyszer, csak a másik irányba:
Ezek az érvek érvényesek nemcsak a rendszeres piramis, hanem a piramis. alsó részének magassága, amely a központ köré írt kör az alapja a piramis.