Curves másodrendű
Másodrendű görbék a síkban említett vonalak által meghatározott egyenletek, amelyekben az x és y koordinátákat, amely a második fokozatot. Ezek közé tartozik egy ellipszis, hiperbola és parabola.
Az általános formája a másodrendű görbe a következő:
ahol A, B, C, D, E, F - száma, és legalább az egyik együtthatók A, B, C nem egyenlő nullával.
A problémák megoldására a görbék a másodrendű leggyakrabban tekintik kanonikus egyenlete egy ellipszis, parabola és a hiperbola. Ezek könnyen megy az általános egyenletek, akkor kell fordítani a problémákat az 1. példa kihagyásokkal.
Meghatározása az ellipszis. Az ellipszis a készlet minden pont a síkon úgy, hogy a távolságok összege a pontot nevezik gócok állandó és nagyobb, mint a távolság a foci.
Fókuszok vannak jelölve, mint az alábbi ábrán.
Canonical egyenlet egy ellipszis:
ahol a és b (a> b) - .. ellipszis hosszúságú, hogy a fele a hossza szegmensek levágja az ellipszis a koordinátatengelyeken.
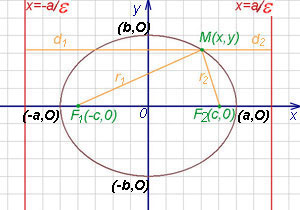
A vonal áthalad a gócok az ellipszis, a szimmetriatengelye körül. Egy másik szimmetriatengelye az ellipszis az a vonal áthalad a középpont merőleges ebben a szegmensben. A lényeg a metszéspontja ezeket a sorokat a központja szimmetria az ellipszis, vagy egyszerűen csak a az ellipszis középpontját.
A vízszintes tengelyen metszi a ellipszis pontokon (a O.) és (-. A O), és az ordináta tengely - pontok (b O.) és (-. B G). Ez a négy pont csúcsoknak nevezzük az ellipszis. A szegmens közötti csúcsok az ellipszis az x tengelyen az úgynevezett fő tengelye, és az ordináta tengely - kisebb tengelye. Hosszuk felülről, hogy a központ az ellipszis nevezik félig-tengely.
Ha a = b. akkor az egyenlet formájában egy ellipszis. Ez az egyenlet a kör sugarát. Így a kör - a speciális esetben ellipszis. Az ellipszis lehet beszerezni a kerülete, a sugarú. ha nyomjon meg egy / b alkalommal a tengely mentén Oy.
Példa 1. Annak ellenőrzése, hogy a vonal által meghatározott általános egyenlet szerint, ellipszis.
Határozat. Gyártunk a teljes konverzió egyenletet. Alkalmazzuk a átadása a szabad kifejezés a jobb oldali, Terminusonként részlege a egyenletet az azonos számú és csökkentve frakciók:
Válasz. Az így kapott egyenlet az átalakulás egyenlete az ellipszis kanonikus. Ezért ez a vonal - ellipszis.
2. példa létrehozása kanonikus egyenlete ellipszis, ha annak ellipszis rendre a 4. és 5..
Határozat. Nézzük a kanonikus képlet uraveniya ellipszis és a helyettesítő: fél nagytengely - egy = 5 kisebb ellipszisféltengelyek - jelentése b = 4 szerezzük be a szükséges kanonikus egyenlete ellipszis: