A tulajdonságait a medián egy háromszög, példákkal

A medián a háromszög - a szegmens összekötő csúcsa a háromszög, hogy a közepén az ellenkező oldalon.

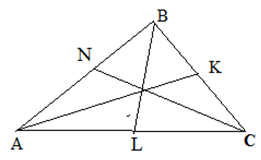
A tulajdonságait a háromszög középvonalainak

1. A medián osztja a háromszög két egyenlő méretű háromszög (vagyis háromszögek ugyanazon a területen).
2. A a háromszög középvonalainak metszik egymást egy pont, amely osztja mindegyikük arányban 2: 1, a tetejétől kezdve. Ez a pont az úgynevezett súlypontja a háromszög.
3. Egész háromszöget van osztva hat a medián egyenlő háromszögek.
4. Egy egyenlő szárú háromszög, medián, csökkent a bázis felezi és magasságát.
5. Egy szabályos háromszög bármely átlagos magasságuk és a felezővonal.

Példák problémák megoldása

Egy szabályos háromszög, melynek az oldalán, hogy a medián végzett cm. Mekkora területű háromszöget.

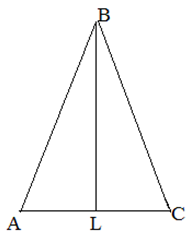
A medián osztja a háromszög két egyenlő-háromszög, majd, ahonnan

Mi található a háromszög területe. Mivel a háromszög egyenlő szárú, a medián a magassága, azaz a Triangle - téglalap és négyzet

A Pitagorasz-tétel lelet befogó:

Behelyettesítve ezeket az eredményeket a Eq felületek:

Most azt látjuk, a háromszög területe:

Egy oldalú háromszög, látni, látni, és volt egy átlagos szög és pontban metszik egymást. Find.

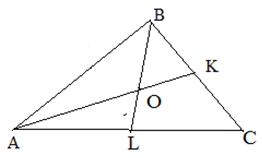
Mivel - háromszög medián, majd

Képzeljünk el egy háromszöget. A tétel az koszinuszok találni

Medián és pontban metszik egymást, amely megosztja mindegyikük arányban 2: 1, kezdve a felső, azaz,