A szög a síkok közötti
A szög a két különböző síkban meghatározható bármely kölcsönös elrendezése a síkon.
Triviális esetben, ha a sík párhuzamos. Ezután a köztük lévő szög a nullának tekintjük.
Nem triviális eset, amikor a sík metszi egymást. Az alkalom és elkötelezett a további vitát. Először is, szükségünk van a fogalmát dihedráiis szög.
9.1 diéderes szög
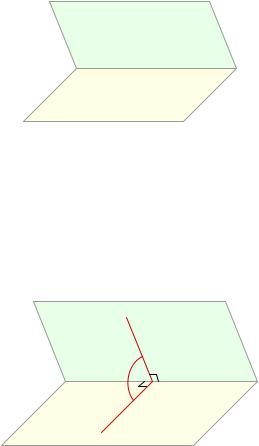
A diéderes szög közös két fél-line (amely az úgynevezett egy él diéderes szög). Ábra. 50 ábrázolja a diéderes által bezárt szög fele-síkok, és a; szélén a diéderes szög a vonal egy, a teljes a fél-sík adatainak.
Ábra. 50. A diéderes szög
A torziós szög fokokban mérve vagy radiánban szó, szögekre adjon a torziós szög. Ez történik az alábbiak szerint.
A szélén a diéderes által bezárt szög félsíkra. egy tetszőleges ponton M. Draw sugarak MA és MB, illetve fekszenek ezek a fél-síkok, és merőleges a szélén (ábra. 51).
Ábra. 51. Lineáris szög diéder
A kapott szög AMB lineáris diéderes szög. Szög „= \ AMB pontosan mi szögértéke diéderes szög.
Definíció. Corner diéderes szög a méret a lineáris szög a diéderes szög.
Minden lineáris diéderes szög egyenlő egymással (mert kapunk egymástól párhuzamosan eltolódik). Ezért, a jelen meghatározás helyes: az érték nem függ az adott választott az M pont a szélén a diéderes szög.
9.2 meghatározása a szög a síkok közötti
A kereszteződésekben a két sík kapunk négy dihedráiis szöget. Ha mindannyian ugyanazt az értéket (90), az úgynevezett merőleges síkban; akkor a szög a síkok közötti 90.
Ha nem az összes diéderes szög egyenlő (azaz, két akut és két tompa), a szög a síkok közötti értékének nevezzük az akut diéderes szög (ábra. 52).
Ábra. 52. A szög a síkok közötti
9.3 Példák problémák megoldására
Nézzük a három feladat. Az első egyszerű, a második és a harmadik körülbelül C2 szintű a matematika vizsga.
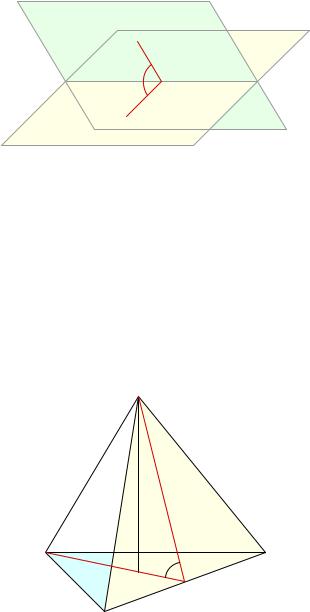
Probléma 1. Keresse meg a szög a két arca szabályos tetraéder.
Határozat. ABCD egy szabályos tetraéder. Döntetlen medián AM DM és a megfelelő arcok, és a magassága a tetraéder DH (ábra. 53).
Ábra. 53. Probléma 1
Medián, AM és DM is a magasban az ABC és a DBC egyenlő oldalú háromszög. Ezért, a szög „= \ AMD lineáris diéderes által bezárt szög az arcok ABC és a DBC. Találunk azt DHM háromszög: