A sugara a beírt kör a gyémánt - képletű számítási példákban

Rhombus - egy paralelogramma, amelynek minden oldala egyenlő. Ezért örökli az összes tulajdonságait paralelogramma. nevezetesen:

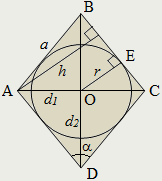
• Átlói rombusz merőlegesek.
• Átlói rombusz a szögfelezői a belső szögek.

Egy kör írható, a négyszög akkor és csak akkor, ha az összeg a szemközti oldalai egyenlők.
Ezért lehessen helyezni egy kör minden gyémánt. Központja a beírt kör egybeesik a központja a kereszteződésekben a átlói rombusz.
A sugár a beírt kör gyémánt lehet kifejezni többféleképpen

1 módja. A sugár a beírt kör magasságában a gyémánt keresztül

Rombusz magassága megegyezik az átmérője a beírható kör. Ez következik a tulajdonságait a téglalap, hogy létrehozzák a beírt kör átmérője és magassága rombusz - átellenes oldalakon a téglalap egyenlő.

Formula így a sugara a beírt kör a magassága a gyémánt keresztül:

2 módszer. A sugár a beírt kör a gyémánt keresztül az átlós

A terület a rombusz fejezhető ki a sugara a beírt kör
, ahol P - kerülete a rombusz. Annak ismeretében, hogy a kerület az összege minden oldalról a téglalap, van p = 4 × a. majd
De rombusz területe is egyenlő fél termékét átlók
Prirovnyat jobb része a terület képletek, mi a következő egyenlőség
Az eredmény egy olyan képletet a sugara a beírt kör a gyémánt keresztül az átlós

Példa a kiszámításakor a sugara beírható kör a rombusz ha ismert átlók
Keresse meg a kör sugarát írt a rombuszt, ha ismert, hogy az átlós hossza 30 cm és 40 cm
ABCD -romb, ha az AC és BD átlók. AC = 30 cm, BD = 40 cm
Let O pont - a központ a rombusz ABCD írt egy kört, akkor is egy metszéspontja az átlók, amely elválasztja őket félbe.


tk átlói metszik rombusz derékszögben, a háromszög AOB derékszögű. Ezután szerint a Pitagorasz-tétel
, szubsztituált a általános képletű a korábban kapott értékeket

AB = 25 cm
Alkalmazása a korábban levezetett képlet a sugara a körülírt a gyémánt kapjunk

3. módszer. A sugara a beírt kör a gyémánt keresztül szegmensek n és m

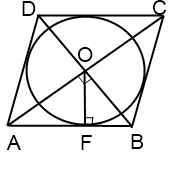
Point F - érintési pont a kör egy oldalon a rombusz, amely osztja azt szegmensekre AF és BF. Legyen AF = m, BF = n.
O pont - középpontján átmenő átlóinak rombusz és a központ a beírható kör is.
AOB háromszög - négyzet átlós rombusz metszik derékszögben.
, mert Ez a sugár felhívjuk az érintési pont a kör. Következésképpen - magassága a háromszög átfogója AOB. Ezután AF és BF - vetülete a lábát a átfogója.
Magasság egy derékszögű háromszög, az átfogó csökkentjük arányos az átlagos között előrejelzések a lábát a átfogója.

Képlet sugara a beírt kör a gyémánt szegmensek négyzetgyökével a termék ilyen szegmensek, amely elválasztja az oldalán a rombusz érintési pont kerületének

Példa a kiszámításakor a sugara beírható kör a rombusz ha ismert hosszúságú m és n
Keresse meg a kör sugarát egy rombusz, ha az érintési pontját osztja a rombusz oldala 9 és 4
ABCD -romb, ha az AC és BD átlók.
Hagyja az O pont - a központja a rombusz ABCD írt egy kört.
Hagyja, hogy a F pont - érintési pont a kör oldalán rombaAB. Aztán. AF = 9, BF ​​= 4
Alkalmazása a korábban kapott általános képletű,