A pontok helye - studopediya

Definíció.

Pontok helye (a továbbiakban: HMT), az úgynevezett az ábra síkjára, amely pont, amely bizonyos tulajdonság, és nem tartalmaz semmilyen pontot, amely nem rendelkezik ezzel a tulajdonsággal.

Mi csak azokat GMT, amely lehet kialakítani vonalzóval és iránytű.

Tekintsük a locus a gépen a legegyszerűbb és leggyakrabban fejezi az ingatlan:

1) lókusz, egymástól egy adott távolságban r ettől a ponttól O egy kör közepén a ponton r sugarú.

2) a locus egyenlő távolságra a két adat pont, A és B jelentése egy vonal merőleges a AB szakaszt és áthatol a közepén.

3) lókusz egyenlő távolságra két egymást metsző adatvonalak van egy pár egymásra merőleges vonalak átmenő metszéspontja, és elosztjuk a szögek között egyenes felét.

4) lókusz, egymástól egyenlő távolságra h a vonal, van két egyenes vonal párhuzamos az egyenes vonal, és található mindkét oldalán vele a h távolságot.

5) A lókusz a központok körök kapcsolatos, hogy a vonal m az M pont rajta, merőleges AB M pont (kivéve az M pont).

6) A lókusz központja körök kapcsolódó kör ebben a rajta ochke M, jelentése egy egyenes, amely áthalad az M pont és a központ a kör (kivéve a pontokat M és O).

7) lokuszt, amely az aktív szegmens látható egy adott szögben, a két körívek leírt ebben az intervallumban és mellékelve egy adott szögben.

8) lókusz, a távolság, amely a két adat pont, A és B jelentése az áttétel m. n, egy kör (úgynevezett Apollóniusz kör).

9) A lókusz az a felezőpontja az akkordok levonni az egyik pont a kör a kör épített összekötő szakasz ezen a ponton, hogy a közepén a kör, mint átmérője.

10) A lókusz az a csúcsai a háromszög egyenlő ezt, és egy közös alap, két egyenes párhuzamos a földre, és áthalad a csúcsa a háromszög, és ez szimmetrikus tartalmazó sor a bázis.

Íme néhány példa a megállapítás a locus.

Példa 2.Find HMT hogy felezőpontja akkordok levonni egy ponton a kerülete (locus № 9).

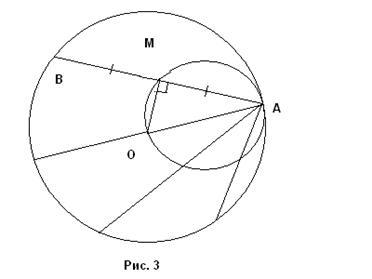
Határozat. Adott egy O középpontú kör és a kör választott pontból amelyek birtokában akkord. Megmutatjuk, hogy a kívánt lókusz egy kör épül AB átmérőjű (kivéve a A pont) (3.).

Let AB - egy bizonyos akkord és M - évei közepén. Csatlakoztatása M és O. Ezután IO ^ AB (sugár, akkord osztja ketté, amely merőleges erre a húrt). de aztán ÐAMO 90 = 0. Ezért M tartozik kör átmérőjű AB (HMT № 7). mert ez kör átmegy az O pont, akkor a G tartozik a locus.

Megfordítva, tegyük fel, hogy M tartozik a locus. Aztán fürdőzés után a M akkord AB összekötő M és O, azt találjuk, hogy ÐAMO = 0. 90 azaz MO ^ AB, ami azt jelenti, hogy az M - a közepén a akkord AB. Ha M egybeesik a G, O - AC közepén.

koordinálja a módszer gyakran lehetővé teszi, hogy megtalálja a pályája.

Példa 3.Nayti HMT, a távolság, amely a két adat pont, A és B jelentése ebben a tekintetben m. N (m ≠ n).

Határozat. Mi válasszon egy derékszögű koordináta-rendszert úgy, hogy a A és B pontok található az x-tengely körül szimmetrikusan eredetét, és az Y tengely közepén halad át az AB (4. ábra). Hagyja, AB = 2a. Ezután az A pont koordinátái A (a, 0), B pont - A koordináták (-a, 0). Tegyük fel, hogy C tartozik a lókusz, koordináták C (x, y) és a CB / CA = m / n. de eszköze

Mi átalakíthatja egyenlőséget. van

Expanzió után zárójelben és csökkenti hasonló kifejezések, megkapjuk

Osszuk a bal és jobb oldalon a egyenlőtlenség (ez megtehető, hiszen a feltételezés), majd válassza ki a tökéletes négyzet, hogy x. kap

De az utolsó egyenlet definiál egy kör közepén és sugár tehát, ha a pont kielégíti a probléma, akkor tartozik (**).

Megfordítva, tegyük fel, hogy a pont koordinátái (x, y) kielégíti a egyenletet (**). Ezzel valamennyi számítást az ellenkező irányba, megérkezik az egyenlet (*), ami azt bizonyítja, hogy a pályája a lényeg.