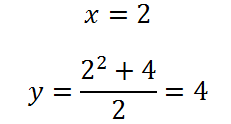A maximális és minimális értékek a funkciók az intervallumban
Jó napot minden kedves olvasónknak!
Ebben a cikkben megpróbáljuk megtanulni, hogyan kell meghatározni a maximális és minimális értékei a különböző funkciók egyszerű és bonyolultabb, találni szélsőérték pont, annak megállapítására, hogy a szélsőséges érték minimum vagy maximum funkciók, és még megkülönböztetni az inflexiós funkciója a végletekig.
mi jár az alábbiak szerint:
1. Határozza meg a függvény deriváltját.
2. egyenlővé a származék nullára annak meghatározására, hogy a szélsőértékek a funkció (ha a kapott egyenletnek gyökerek). Határozza meg, hogy az adatok tartoznak a végletekig a megadott időközönként.
3. Ha a funkció extrémuma előre meghatározott időközönként, megállapítására, hogy magas vagy alacsony.
4. Ha a funkció nincs szélsőérték (nincs gyökereit egyenletek kapott egyenlővé a származék nullára), meghatározzák a jele a származékot. Ez megmutatja nekünk e vagy sem a funkciója növekszik vagy csökken. Ezután folytassa a feltétellel a probléma: ha a funkció növeli a maximális érték a jobb oldalon, és a minimális - a bal oldalon. Ha csökken - éppen ellenkezőleg. problémamegoldás segít mindannyiunkat kereshetőség, és a képek segítségével, igyekszünk, hogy ne hagyja el a homályos helyek ilyen jellegű problémák megoldását.
Probléma 1. Meg kell határozni a legnagyobb értéke a függvény:
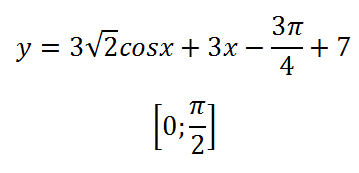
Mi működik az algoritmus alapján, először meghatározzák a származék. Itt van az összeg a funkciókat, így definiáljuk a származékot külön-külön, és add fel, majd egyenlővé a származék nullával:
Mi megoldjuk a kapott egyenletet. Ha a gyökerek - akkor, talán, mi szélsőséges (az a pont, ahol a derivált nulla, nem lehet extrémuma és az inflexiós pont).
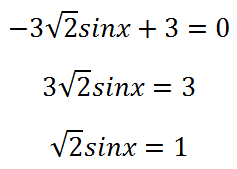
Látjuk - gyökér:
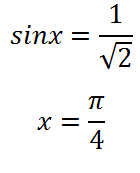
Ezen a ponton a funkció egy extrém. Fontos, hogy ez a pont tartozik egy adott intervallumban. Keresse ki a legjobban ezt vagy minimum.Dlya meg kell határoznia a jele a származékos szomszédságában ezen a ponton, azaz a jobb és bal oldali is. Például, akkor megteszi a lényeg - ez a bal oldalon, és a lényeg - ez lesz a jobb. majd:
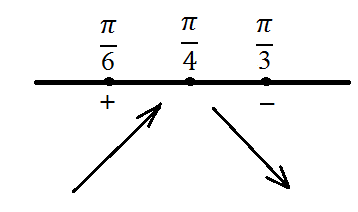
Egyértelmű, hogy a függvény maximális értéke a ponton maksimuma.Naydem ez az érték a következő: Behelyettesítve a pont szélsőérték funkció az egyenletben:
V: A legnagyobb érték a függvény egy adott intervallum 10.
2.Find legkisebb függvényérték meghatározott időközönként:
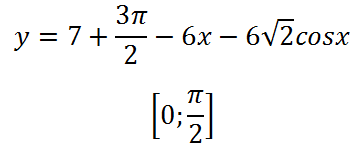
Ugyanígy, mint az első alkalommal, vesszük a derivatív és zérus:
Már világos, hogy ez az egyenlet a gyökerek:
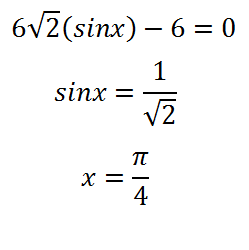
Azon a ponton, a függvénynek egy extrém. Maximum és minimum? Keressük az érték a származékos jobb és bal oldalán a lényeg. Ismét egy pontot - ez lesz található a bal oldalon, és a lényeg - ez lesz a jobb. majd:
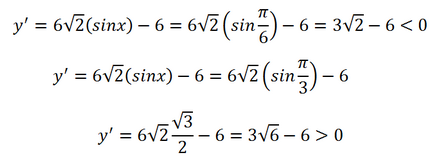
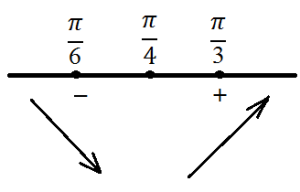
Függvény a legkisebb érték a ponton m inimuma úgy találjuk, hogy:
Válasz: A legkisebb érték a függvény ebben az intervallumban 1.
Nézzük megoldani a következő problémát:
3. Határozza meg a legnagyobb értéke az intervallum:
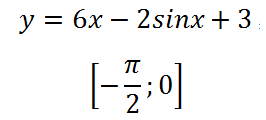
Először is, mint mindig, a származtatott:
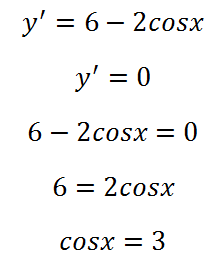
Ez az eset áll fenn, amikor a szélsőértékek a funkció ebben az intervallumban van: a fenti egyenletnek nincs gyökere. Ez azt jelenti, hogy a függvény monoton sem csökken vagy növekszik. Mi lehet meghatározni ezt a jele a származtatott, ha a derivált pozitív - ez a funkció növeli, ha negatív - csökken. Miért van szükségünk, hogy ismerjük a függvény növekszik vagy csökken? A tény az, hogy ha a funkció növeli, értéke mindig nagyobb lesz, a jobb oldalon az intervallum, és csökken, ha - a bal oldalon.
Hazánkban nem számít, milyen szögben vesszük, hisz ez kevesebb, mint 1, így a derivált pozitív, ami azt jelenti, hogy a funkció növeli. Így a maximális értéket el nem éri a 0 pont:
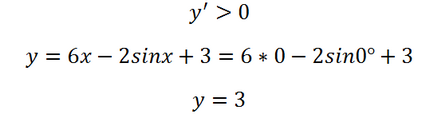
4. Határozzuk meg a minimális érték a funkciót a szegmensben:
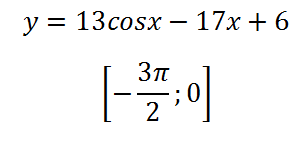
Mi határozza meg a derivatív és nullának:
Már világos, hogy a függvény monoton (nincs gyökerei a kapott egyenlet):
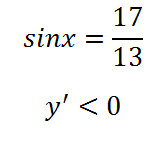
Mivel a származék negatív, akkor arra a következtetésre jutunk, hogy a funkció csökken. Ezután a legalacsonyabb értékre - a jobb végén a szegmens, azaz 0:
Válasz: A legkisebb érték a függvény egy adott intervallum - 19.
5. Keresse meg a legkisebb érték a funkciót a szegmensben:
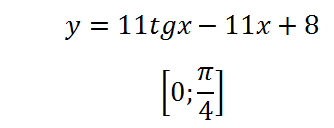
Vegye származék nullának és oldja meg a kapott egyenletet:
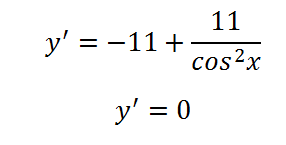
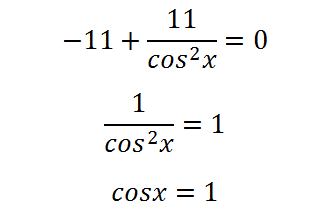
Úgy tűnik - az egyenletnek gyökereket, így a függvény egy extrém értéket ebben a szegmensben (a második gyökere ebben a szegmensben nem tartozik, így nem kell figyelembe venni). Adjuk meg a maximális vagy minimális az. Az 1 érték a koszinusz - a maximális, azaz bizonyos ponton, vagy egy nullához közeli - a koszinusz - abszcissza - kevesebb lesz, mint nulla. Ugyanakkor! Származtatott nulla jel pont nem változik! Ez pozitív szomszédságában nulla, majd függvényében növekszik nulla, és utána. Tehát a függvény a ponton a nulla nincs szélsőérték és inflexiós.
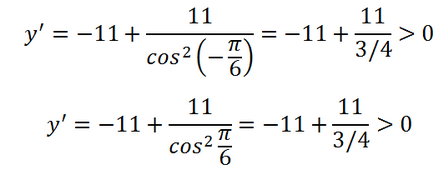
Ezért, hogy meghatározzák a legalacsonyabb érték, meg kell venni a bal szegmenshatáron és számolja a függvény ezen a ponton. By szerencsés egybeesés, ez nulla pont. Azonban lehet, hogy egy másik pontján nullától eltérő, és akkor lehet, hogy egy hiba, figyelembe véve a nulla pontja extrémuma és értékének meghatározása egy függvény benne. Így, az értéke a függvény:
Válasz: A legkisebb érték a függvény egy adott intervallum - 8.
6. Keresse meg a legmagasabb pont funkció:
Az algoritmus feladatok végrehajtásához azonos. Először is - a származék. Itt van a termék a két funkciót, így vesszük a származék a szabály figyelembe a származtatott termék jellemzői:
További egyenlővé ezt a kifejezést a nullához. Egyértelmű, hogy a kitevő mindig nem negatív, bizonyos fokú vagy összeállításra, így a gyökér a „rejtett” a második tényező:
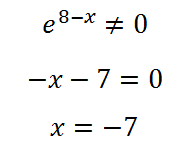
Győződjön meg arról, hogy ez a szélsőérték - maximum. Sőt, ezen a ponton a származtatott jel változik, és változik a pozitív negatív, azaz eddig a pontig a függvény növekszik, és miután - csökken.
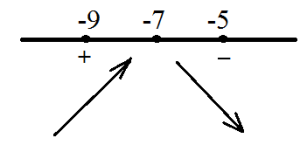
7. Keresse meg a legkisebb érték a funkciót a szegmensben:
Mi lesz, mint mindig, hogy megtalálják a származékot ezt a funkciót, és ez a funkció összetett: a logaritmus fokban kifejezett (és egy bizonyos fokú - még ha amitől aláírja a log, meg kell, hogy tegye a jel modult, hogy ne csökkenjen a meghatározását funkció!). Ezért, annak érdekében, hogy ne felfedje a modul, fel tudjuk használni a szabályt figyelembe a származtatott összetett funkció:
A kapott expressziós van beállítva egyenlő nullával:
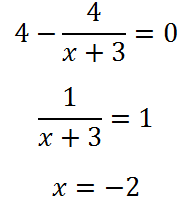
Megjegyezzük, hogy a (3) pontban a származék nincs definiálva. Mindazonáltal, ezen a ponton a származtatott előjelet. Point (-2) - minimális funkció, mivel deriváltja elõjelet negatívból pozitív. Ennélfogva, ezen a ponton a függvény legkisebb értékét. Helye:
Válasz: A legkisebb érték a függvény egy adott intervallum - 8.
8. Keresse meg a legmagasabb pont funkció:
Mi határozza meg a származék egy összetett függvény. Talált egyenlővé a származék nullára:
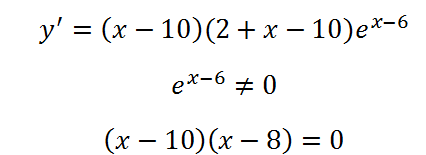
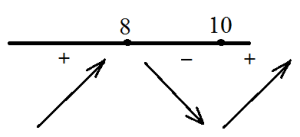
Van két pont a szélsőségek. Egyikük - a legnagyobb, a másik - legalábbis.
Funkció maximum 8.
9. Keresse meg a minimum pont a funkció:
Határozzuk származékos műveket, továbbá, a kitevőt egy komplex funkció (itt, a származék milyen mértékben emelkedett a kitevő értéke 1). Talált egyenlővé a származék nullára:
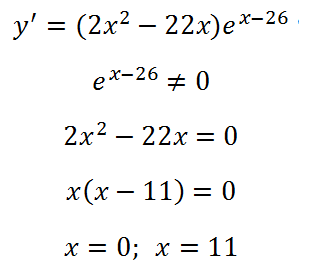
A legkisebb pont a függvény a 11. pontban Ez látható: a származék változik jelentkezzen mínusz plusz.
Válasz: x = 11.
10. Keresse meg a minimális és a maximális pontot a függvény:
Mi határozza meg a származék egy összetett függvény. Talált egyenlővé a származék nullára:
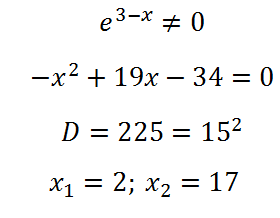
A származék Ez a funkció megváltoztatja jele a negatív pozitív 2. pont (minimum) és a kizáró és pozitív - a 17 (maximum).
11. Keresse meg a legkisebb érték a funkciót a szegmensben:
Megjegyezzük, hogy a kifejezés alatt logaritmus értéke nullánál nagyobb. Ezután 0 "cím =" x + 3> 0 "/> [/ pmath], -3" cím = "x> -3" /> [/ pmath]. Szegmens, amely meg fogjuk vizsgálni, és meghatározza a funkciója a származékos jelek megfelel domain a funkciót.
Keressük a derivatív és nullának:
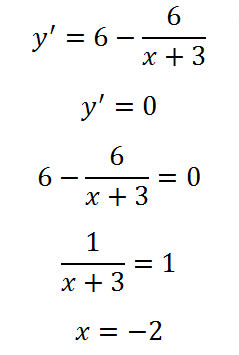
A 2. pontban a származék előjelet, akkor szélsőséges. Megváltoztatja jel a negatív pozitív, ezért ezen a ponton - a minimális pontot. Tart a legkisebb érték a függvény:
Válasz: A legkisebb érték a függvény egy adott intervallum - 8.
12. Keresse meg a legkisebb érték a funkciót a szegmensben:
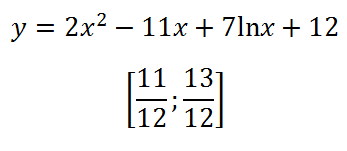
Keressük a derivatív és nullának:
Lehet jegyezni, hogy a funkció domén - pozitív értékeit x (mint a kifejezés a logaritmus nullánál nagyobb), és hogy a származék a ponton 0 nem opredelena.Poluchim másodfokú egyenlet, amelyben az összege az együtthatók értéke 0 (a + b + c = 0) . Ebben az egyenletben, az egyik gyökér 1 és a második C / A:
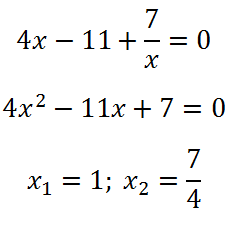
Tegyen fel egy szegmens tartozik, hogy csak egy pontot - 1. A származékos itt megváltoztatja jel negatívról pozitívra, és így ez a minimum. Mi határozza meg a függvény ezen a ponton:
13. Keresse meg a legkisebb érték a funkciót a szegmensben:
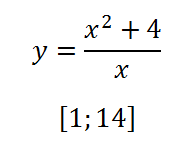
Megjegyezzük, hogy a függvény nincs definiálva a 0 pont.
Vesszük a származékot frakció:
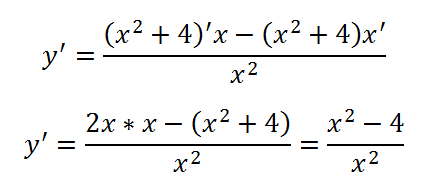
Azonosítjuk a származék nulla, és keressük a gyökerek:
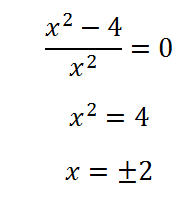
Az egyik gyökerek nem érdekel minket, mert a különbség nem tartozik, és a második pont a származtatott előjelet a negatív polozhitelnyy.To függvényében minimális ezen a ponton. Határozzák meg a minimális érték: