A lineáris függőség a vektorok
Meghatározása lineáris függetlenség vektorok
A1 vektorok rendszer. A2. Egy úgynevezett lineárisan független. Ha egy lineáris kombinációja ezen vektorok À, 1 * A1 + λ2 * A2 +. + Λn * Egy egyenlő a nulla vektor csak a nulla számsor λ1, λ2. λn. azaz, az egyenletrendszert: A1 X1 + A2 x2 +. + Xn = θ csak a triviális megoldás.
Ellenőrizze, hogy a rendszer lineárisan függ vektorok
1. Készíts egy egyenletrendszert:
2. Oldja meg a Gauss. Jordan átalakító rendszer táblázatban vannak felsorolva 29.1. Kiszámításakor a jobb oldalán a rendszer nem rögzíti, mivel ezek a nulla és Jordan nem változik a konverzió.
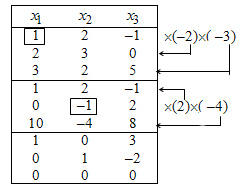
3. Az elmúlt három táblázat sorait írja a rendszer lehetővé teszi, amely egyenértékű az eredeti rendszer:
4. Kap az általános megoldás:
5. Adjuk belátása értéke a szabad változó x3 = 1, megkapjuk a privát triviális oldat X = (- 3,2,1).
A: Így nem nulla számok halmaza (-3,2,1) a lineáris kombinációja az vektorok egyenlő nullával vektor -3A1 + 2A2 + 1A3 = θ. Következésképpen, a rendszer a vektorok lineárisan függ.
A tulajdonságait vektor rendszerek
Az ingatlan (1)
Ha a rendszer a vektorok lineárisan függ, akkor legalább az egyik vektorok bővült másik és, éppen ellenkezőleg, ha legalább az egyik a vektorok a rendszer bővíthető a többi, a rendszer a vektorok lineárisan függ.
Az ingatlan (2)
Ha bármelyik alrendszer vektorok lineárisan függő, akkor az egész rendszer lineárisan függ.
Az ingatlan (3)
Ha a rendszer lineárisan független vektorok, akkor bármely alrendszer lineárisan független.
Az ingatlan (4)
Bármely rendszer vektorok tartalmazó nulla vektor lineárisan függ.
Az ingatlan (5)
A rendszer m-dimenziós vektorok mindig lineárisan függ, ha n értéke nagyobb, mint a vektorok számát a dimenzió (n> m)
Basis vektor rendszer
r - a vektorok számát tartalmazza az alapot.
Tétel 29.1 A készülékről alap vektorok rendszert.
Ha a rendszer m-dimenziós vektorok, amelyek m más egység vektorok E1 E2. Em. ezek képezik az alapját a rendszer.
Az algoritmus megtalálása rendszer alapján vektorok
Annak érdekében, hogy megtalálják a alapján vektorok A1, A2. Egy szükséges:
- Készítsen egy megfelelő vektor rendszert homogén egyenletek A1 X1 + A2 x2 +. + Xn = θ
- Hogy ezt a rendszert
