A harmadfokú egyenlet, algebra

A grafikon a harmadfokú függvényt hívjuk harmadfokú parabola.

Először is, úgy a tulajdonságok és a grafikon a harmadfokú egyenlet y = x³ (ha a = 1).

1) mezőmeghatározásainak - a valós számok halmazán:

2) értéktartomány - összes valós szám:

3) A függvény nulla:

4) O pont (0, 0) köbös parabola osztja két egyenlő részre, amelyek mindegyike úgynevezett ága a köbös parabola. Cubic parabola ágai szimmetrikus O pont - eredetű.

Ebből következik, hogy az ellenkező x értékek megfelelnek az ellenkező y értékei: (- x) ³ = - x³.

5) Ez a funkció növeli a teljes számegyenesen.

6) Az intervallumok állandó megjelölés: a függvény pozitív értékek, amikor x∈ (0; ∞) (vagy y> 0 X> 0);

függvény egy negatív értéket, amikor x∈ (-∞; 0) (vagy y<0 при x<0).

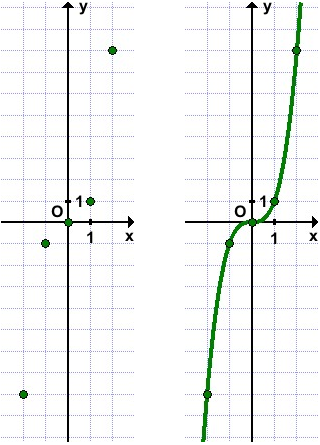
A konstrukció a grafikont a harmadfokú egyenlet, hogy több pontot.

Vegyük pont abszcissza x = 0, x = ± 1, X = ± 2, X = ± 3, és megtalálja a megfelelő érték a funkció:

y = 0 ³ = 0; y = 1 ³ = 1; y = (- 1) ³ = -1; y = 2 ³ = 8; y = (- 2) ³ = -8.

Kapott pont koordinátái (0, 0), (1, 1), (-1, -1), (2, 8), (-2, -8).

Célszerű, hogy regisztrálja a számítások eredményei egy táblázatban:

Ezek a pontok a megjegyzés a koordinátarendszerben, és elkészítjük a harmadfokú parabola:

A grafikon y = ax³ amikor egy ≠ 1 (a ≠ 0) kapunk a függvény grafikonját y = x³ segítségével geometriai transzformáció.

A függvény y = x³ - egy speciális esete hatványfüggvénnyel

ahol α - bármilyen valós szám.

Ennek során az algebra, a különleges esetekben az hatványfüggvény már találkozott a másodfokú függvény y = x² és funkciója fordított arányosság