A hallgatók felkészítése a vizsgát a képzési központ felbontású (referencia Matematika - geometria

• Céljai érdekében
• másodfokú trinomiális
• Egyenletek és egyenlőtlenségek
  modulokkal
• Számtani és mértani sorozat
• koordináta módszerrel
  a gépen
• Ábrák egy koordináta által meghatározott sík egyenlőtlenségek
• Megoldás algebrai egyenletek
• A megoldás a racionális egyenlőtlenségek
• A döntés irracionális egyenlőtlenségek
• Megoldás az exponenciális egyenletek
• Megoldás bemutató egyenlőtlenségek
• Megoldás logaritmikus egyenletek
• Megoldás logaritmikus egyenlőtlenségek
• az egyenletrendszert
• Megoldás trigonometrikus egyenletek
• Trigonometry vizsga
  matematika
• Fokú racionális kitevő

HIVATALOS oktatási anyagok

Piramis, feliratos a szférában. Tulajdonságok a piramis, a gömb feliratos

1. meghatározása a piramis, feliratos a gömb, az úgynevezett piramis. összes csúcsai a gömb (ábra. 1).

DEFINÍCIÓ 2. Ha a piramis van írva a gömböt, a gömb le a piramist.

1. Tétel a piramis köré lehet leírni a körét és csak akkor, ha a fenék közelében a piramis lehet leírni, mint egy kör.

Bizonyítás. Először megmutatjuk, hogy ha a piramis feltüntetik egy gömb körül az alap lehet leírni, mint egy kör. Ehhez vizsgálni a 2. ábra.

A 2. ábra egy piramis SA 1 A 2. An. feliratos a szférában. Piramis bázis metszi a gömböt egy kör mentén ami bele van írva a sokszög A 1, A 2 An - alapja a piramis. Ez bizonyított.

Tegyük fel, hogy a fenék közelében az A 1 A 2 A piramis SA 1. 2. lehet leírni, mint egy kör. Megmutatjuk, hogy ebben az esetben körülbelül piramis SA 1. 2. leírható egy gömb. Ebből a célból, jelöljük központja körülírt sokszög A 1, A 2. An. szimbólum O „és rajzol egy egyenes vonal p, áthaladva az O pont”, és merőleges arra a síkra, a sokszög A 1, A 2. (3.).

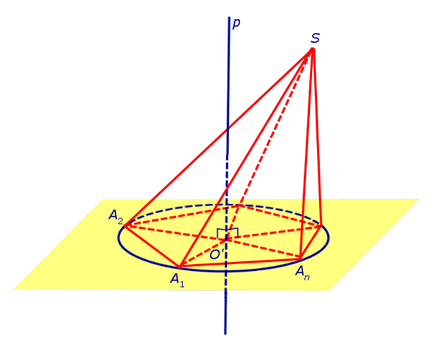
Tekintsük β áthaladó sík SAn felezőpontja, és merőleges a szegmensben. Ha az O betű jelöli a metszéspont β síkjával a sor p, az O pont a központja a gömb leírt körülbelül piramis SA 1 a 2. An. Ennek bizonyítására tekintsük a következő: 4. ábra.

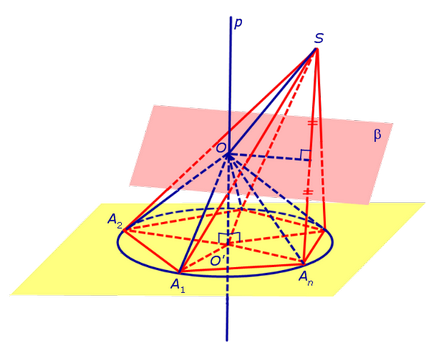
Megmutatjuk, hogy egy O pont található azonos távolságra pontokat S, A 1. A 2. An. Mivel az O pont fekszik a függőleges felezővonal SAN. az operációs rendszer és a távolság oan egyenlő. Másrészt, a szegmensek OA 1. OA 2. oan, mint átfogója egyenlő téglalap alakú háromszögek OO'A 1. OO'A 2. OO'An. (Háromszögek OO'A 1. OO'A 2. OO'An egyenlő. Ahogy befogó OO „teljes, és a lábak O'A 1. O'A 2. O'An vannak egyenlő a sugara köré rajzolt kör a sokszög A 1 A 2. An).

Tehát beláttuk, hogy az O pont ugyanolyan távolságra a piramis csúcsára SA 1 A 2. An. Ez azt jelenti, hogy az O pont a központja a gömb leírt körülbelül piramis SA 1 a 2. An.

Hogy teljes legyen a bizonyítás már csak azt kell bizonyítania, hogy a gépet β és a vonal p valóban metszik egymást. Feltételezve, hogy nem ez a helyzet, ezt a feltételezést követi a síkban β és az egyenes vonal párhuzamos a p, és ezáltal az a pont S síkjában fekszik A 1 A 2. An. ami ellentmond a meghatározása a piramis.

Következmény 1. Mintegy bármilyen szabályos gúla leírható hatálya.

2. Következmény Ha az összes oldalsó széleit a piramis egyenlő. valamit róla, akkor írja le az körét.

Megjegyzés. Az alap a merőleges csökkent a csúcsa a piramis annak alapsíkon a középpontja körülbelül alapkör leírt. Lásd bizonyíték.

A gömb sugara leírt a korrekt N - szén piramisok

Probléma 1. A magassága a jobb N - szén piramis h. bázis él hossza megegyezik a. Keresse meg a gömb sugara köré tekerjük a piramis.

Határozat. Tekintsünk egy szabályos n - szén piramis SA 1 A 2. jelöljük az O betű és a központ a gömb leírt a piramisok, és a szimbólum O „- a központ a alapja a piramis. Döntetlen sík SO „An (ábra. 5).

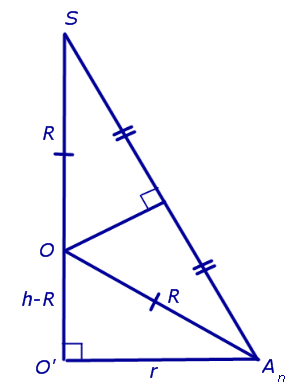
A ábrán az R betű 5 jelöli a gömb sugara a piramis köré, és a levél r - a kör sugara körül alapja a piramis. Szerint a Pitagorasz-tétel háromszög O'O An szerezni